题目内容
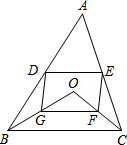
 如图,已知平行四边形ABCD的面积是16,点0是平行四边形ABCD对角线的交点,OE∥AD交CD于点E,OF∥AB于点F,那么△EOF的面积是( )
如图,已知平行四边形ABCD的面积是16,点0是平行四边形ABCD对角线的交点,OE∥AD交CD于点E,OF∥AB于点F,那么△EOF的面积是( )| A、1 | B、2 | C、3 | D、4 |
考点:平行四边形的判定与性质
专题:
分析:由平行四边形ABCD的面积是16,可求得△BCD的面积,又由OE∥AD交CD于点E,OF∥AB于点F,易得△DOE∽△DBC,△BOF∽△BDC,△CEF∽△CDB,然后由相似三角形面积比等于相似比的平方,求得答案.
解答:解:∵平行四边形ABCD的面积是16,
∴S△BCD=
S?ABCD=8,OB=OD,
∵OE∥AD,OF∥AB,
∴△DOE∽△DBC,△BOF∽△BDC,
∴S△DOE=
S△BCD=2,S△BOF=
S△BCD=2,
∴DE=CE,BF=CF,
∴EF∥BD,EF=
BD,
∴△CEF∽△CDB,
∴S△CEF=
S△BCD=2,
∴S△EOF=8-2-2-2=2.
故选B.
∴S△BCD=
| 1 |
| 2 |
∵OE∥AD,OF∥AB,
∴△DOE∽△DBC,△BOF∽△BDC,
∴S△DOE=
| 1 |
| 4 |
| 1 |
| 4 |
∴DE=CE,BF=CF,
∴EF∥BD,EF=
| 1 |
| 2 |
∴△CEF∽△CDB,
∴S△CEF=
| 1 |
| 4 |
∴S△EOF=8-2-2-2=2.
故选B.
点评:此题考查了平行四边形的性质以及相似三角形的判定与性质.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
下列条件能判断两个三角形全等的是( )
①两角及一边对应相等;
②两边及其夹角对应相等;
③两边及一边所对的角对应相等;
④两角及其夹边对应相等.
①两角及一边对应相等;
②两边及其夹角对应相等;
③两边及一边所对的角对应相等;
④两角及其夹边对应相等.
| A、①③ | B、②④ |
| C、②③④ | D、①②④ |
已知a的平方根是±8,则a的立方根是( )
| A、2 | B、4 | C、±2 | D、±4 |
 如图,D、E分别是不等边三角形ABC(即AB≠BC≠AC)的边AB、AC的中点.O是△ABC平面上的一动点,连接OB、OC,G、F分别是OB、OC的中点,顺次连接点D、G、F、E.
如图,D、E分别是不等边三角形ABC(即AB≠BC≠AC)的边AB、AC的中点.O是△ABC平面上的一动点,连接OB、OC,G、F分别是OB、OC的中点,顺次连接点D、G、F、E.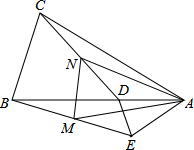 如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,且点B,A,D在一条直线上,连接BE,CD,M,N分别为BE,CD的中点,下列结论:
如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,且点B,A,D在一条直线上,连接BE,CD,M,N分别为BE,CD的中点,下列结论: 已知二次函数y=ax2+bx+c(a≠0)的图象如图,则下列结论中不正确的有( )个.
已知二次函数y=ax2+bx+c(a≠0)的图象如图,则下列结论中不正确的有( )个. 在平面直角坐标系中,已知A(2,0),B(3,1),C(1,3);
在平面直角坐标系中,已知A(2,0),B(3,1),C(1,3);