题目内容
6．
如图，在△ABC中，$\frac{AB}{DB}$=$\frac{AC}{EC}$．求证：（1）$\frac{AD}{AB}$=$\frac{AE}{AC}$；
（2）$\frac{AD}{DB}$=$\frac{AE}{EC}$．
分析 （1）根据比例的性质得到$\frac{AD}{DB}$=$\frac{AE}{EC}$，根据平行线的判定得到DE∥BC，得到答案；
（2）由（1）可得结论．
解答 证明：（1）∵$\frac{AB}{DB}$=$\frac{AC}{EC}$，
∴$\frac{AB-DB}{DB}$=$\frac{AC-EC}{EC}$，即$\frac{AD}{DB}$=$\frac{AE}{EC}$，
∴DE∥BC，
∴△ADE∽△ABC，
∴$\frac{AD}{AB}$=$\frac{AE}{AC}$；
（2）由（1）得$\frac{AD}{DB}$=$\frac{AE}{EC}$．
点评 本题考查的是平行线分线段成比例定理和逆定理以及相似三角形的判定和性质，灵活运用定理、找准对应关系是解题的关键．
练习册系列答案
名校课堂系列答案
相关题目
如图，是一个4×4的方格图，点A，点B都在格点上，要求在格点上再找到一点C，使△ABC为等腰直角三角形，则选择的点C有6个．
17．中华人民共和国国家统计局2003年2月28日统计：综 合国民经济持续较快增长．全年国内生产总值跃上10万亿元的新台阶，达到102398亿元，按可比价格计算，比上年增长8%．（见图）把102 398用科学记数法表示为（ ）亿元．
| A． | 1.02398×105 | B． | 10.2398×104 | C． | 1.02398×106 | D． | 0.102398×107 |
如图，已知DA∥FE∥CB，且DA=CB，求证：$\frac{EA}{AM}$=$\frac{EB}{BN}$．
如图，已知AB⊥AC于点A，DC⊥AC于点C，BE平分∠ABD，DE平分∠BDC，BE的延长线交DC的延长线于点F．求证：AB=CF．
7．
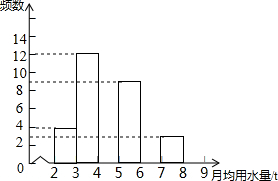旬阳县在实施定额用水管理前，对城镇6000户居民生活用月均用水情况（单位：t）进行了简单随机抽样调查，并将调查结果绘制成频数分布表和频数分布直方图．
（1）补全频数分布表和频数分布直方图；
（2）用扇形统计图表示各用水段居民户占总居民户的百分比；
（3）为了鼓励居民节约用水，县自来水公司要确定一个用水量的标准，超出这个标准的部分按照2倍的价格收费，且要保证60%以上的家庭水费支出不受影响，你觉得家庭月均用水量应定为多少？为什么？在额定标准下，估计有多少户居民家庭水费支出较前有所增加？
旬阳县在实施定额用水管理前，对城镇6000户居民生活用月均用水情况（单位：t）进行了简单随机抽样调查，并将调查结果绘制成频数分布表和频数分布直方图．（1）补全频数分布表和频数分布直方图；
（2）用扇形统计图表示各用水段居民户占总居民户的百分比；
（3）为了鼓励居民节约用水，县自来水公司要确定一个用水量的标准，超出这个标准的部分按照2倍的价格收费，且要保证60%以上的家庭水费支出不受影响，你觉得家庭月均用水量应定为多少？为什么？在额定标准下，估计有多少户居民家庭水费支出较前有所增加？
| 月均用水量 | 频数 | 百分比 |
| 2≤x＜3 | 4 | 8% |
| 3≤x＜4 | 12 | 24% |
| 4≤x＜5 | 14 | 28% |
| 5≤x＜6 | 9 | 18% |
| 6≤x＜7 | 6 | 12% |
| 7≤x＜8 | 3 | 6% |
| 8≤x＜9 | 2 | 4% |
| 合计 | 50 | 100% |