题目内容
1.观察下列各式:1×2×3×4+1=52;
2×3×4×5+1=112;
3×4×5×6+1=192;
判断是否任意四个连续正整数之积与1的和都是某个正整数的平方,并说明理由.
分析 此题可以先假设正确,再用任意四个连续正整数之积加上1进行因式分解,看能否得到一个正整数的平方即可.
解答 解:任意四个连续正整数之积与1的和都是某个正整数的平方.理由如下:
设四个连续的正整数为n、(n+1)、(n+2)、(n+3),
则n(n+1)(n+2)(n+3)+1
=(n2+3n)(n2+3n+2)+1
=(n2+3n)2+2(n2+3n)+1
=(n2+3n+1)2.
点评 本题考查了因式分解的应用,关键是能够用代数式把题中所说的关系式列出来,然后通过运算写成完全平方式的形式,即可证明结论正确.难点在于多项式乘以多项式的运算后,如何化为完全平方式.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
12.下列说法中,正确的是( )
| A. | 延长直线AB | B. | 延长射线OA | ||
| C. | 延长线段AB至C,使AC=BC | D. | 反向延长线段AB至C,使AC=AB |
2.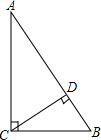 如图,已知AC⊥BC,CD⊥AB,垂足分别是C、D,那么以下线段大小的比较中必定成立的是( )
如图,已知AC⊥BC,CD⊥AB,垂足分别是C、D,那么以下线段大小的比较中必定成立的是( )
 如图,已知AC⊥BC,CD⊥AB,垂足分别是C、D,那么以下线段大小的比较中必定成立的是( )
如图,已知AC⊥BC,CD⊥AB,垂足分别是C、D,那么以下线段大小的比较中必定成立的是( )| A. | AD>CD | B. | BC<AC | C. | BC>BD | D. | BD<CD |
 读句画图:如图,A,B,C,D在同一平面内,
读句画图:如图,A,B,C,D在同一平面内,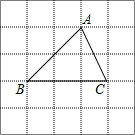 如图所示的方格中,每个小方格都是边长为1的正方形,△ABC是格点三角形(即顶点恰好是正方形的顶点),在图中画出与△ABC有一条公共边BC且全等的所有格点三角形.
如图所示的方格中,每个小方格都是边长为1的正方形,△ABC是格点三角形(即顶点恰好是正方形的顶点),在图中画出与△ABC有一条公共边BC且全等的所有格点三角形. 如图,在△ABC中,$\frac{AB}{DB}$=$\frac{AC}{EC}$.求证:
如图,在△ABC中,$\frac{AB}{DB}$=$\frac{AC}{EC}$.求证: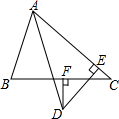 如图,△ABC中,F为BC的中点,FD⊥BC,交∠BAC的平分线于D,DE⊥AC于E,求证:AB+AC=2AE.
如图,△ABC中,F为BC的中点,FD⊥BC,交∠BAC的平分线于D,DE⊥AC于E,求证:AB+AC=2AE.