题目内容
10. 如图在Rt△ABC中,∠A=90°,若BC=10,sinB=0.6,则斜边上的高AD等于4.8.
如图在Rt△ABC中,∠A=90°,若BC=10,sinB=0.6,则斜边上的高AD等于4.8.
分析 首先求出AC、AB,再根据S△ABC=$\frac{1}{2}$•BC•AD=$\frac{1}{2}$•AB•AC,求出AD即可.
解答 解:在Rt△ABC中,∵∠A=90°,BC=10,
∴sinB=$\frac{AC}{BC}$=0.6,
∴AC=6,
∴AB=$\sqrt{1{0}^{2}-{6}^{2}}$=8,
∵S△ABC=$\frac{1}{2}$•BC•AD=$\frac{1}{2}$•AB•AC,
∴AD=$\frac{6×8}{10}$=4.8,
故答案为4.8.
点评 本题考查解直角三角形、锐角三角函数等知识,解题的关键是灵活运用所学知识解决问题,学会用面积法求斜边上的高.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
5.下列不等式变形正确的是( )
| A. | 由a>b,且c≠0,得ac<bc | B. | 若x>y,且m≠0,则-$\frac{x}{m}<-\frac{y}{m}$ | ||
| C. | 若x>y,则xz2>yz2 | D. | 若an2>bn2,则a>b |
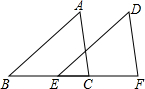 如图,已知B,E,C,F在同一条直线上,且△ABC≌△DEF,BE=3cm,则CF=3cm.
如图,已知B,E,C,F在同一条直线上,且△ABC≌△DEF,BE=3cm,则CF=3cm.