题目内容
13. 如图,Rt△ACD中,∠C=90°,∠CAD=60°,∠CAD的平分线AB交CD于B点,且AB=4cm,那么点B到AD的距离是2cm.
如图,Rt△ACD中,∠C=90°,∠CAD=60°,∠CAD的平分线AB交CD于B点,且AB=4cm,那么点B到AD的距离是2cm.
分析 根据角平分线的性质“角的平分线上的点到角的两边的距离相等”,可得点B到AD的距离是=点B到AC的距离=CB=2.
解答  解:过B作BE⊥AD于E,
解:过B作BE⊥AD于E,
∵∠C=90°,∠CAD=60°,∠CAD的平分线AB交CD于B点,
∴∠CAB=30°,BE=BC
∴BE=BC=$\frac{1}{2}$AB=2cm,
故答案为:2.
点评 本题主要考查三角形角平分线的性质,由已知能够注意到B到AD的距离即为CB长是解决的关键.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案
相关题目
4.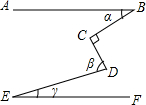 如图,AB∥EF,∠C=90°,则∠α,∠β,∠γ之间的关系是( )
如图,AB∥EF,∠C=90°,则∠α,∠β,∠γ之间的关系是( )
 如图,AB∥EF,∠C=90°,则∠α,∠β,∠γ之间的关系是( )
如图,AB∥EF,∠C=90°,则∠α,∠β,∠γ之间的关系是( )| A. | ∠β=∠α+∠γ | B. | ∠α+∠β+∠γ=180° | C. | ∠α+∠β-∠γ=90° | D. | ∠β+∠γ-∠α=90° |
1.下列说法正确的是( )
| A. | $\frac{1}{81}$的立方根是$\frac{1}{9}$ | B. | -$\frac{1}{81}$的平方根是$\frac{1}{9}$ | ||
| C. | $\frac{1}{27}$的算术平方根是$\frac{1}{3}$ | D. | -$\frac{1}{27}$的立方根是-$\frac{1}{3}$ |
5.两个连续偶数之积为168,则这两个连续偶数之和为( )
| A. | 26 | B. | -26 | C. | ±26 | D. | 都不对 |
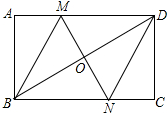 如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BD相交于点N,连接BM,DN.
如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BD相交于点N,连接BM,DN.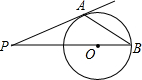 如图,PA切⊙O于A,PO交⊙O于B,若∠P=35°,则∠PBA=27.5°.
如图,PA切⊙O于A,PO交⊙O于B,若∠P=35°,则∠PBA=27.5°. 在一个仓库里堆积着若干个正方体的货箱,要搬运这些货箱很困难,可是仓库管理员要落实一下箱子的数量,于是就想出一个方法:将这堆货箱分别从正面、左面、上面所看到的平面图形画了出来,如图所示,你能根据这些平面图形帮他清点一下箱子的数量吗?这些正方体货箱的个数为( )
在一个仓库里堆积着若干个正方体的货箱,要搬运这些货箱很困难,可是仓库管理员要落实一下箱子的数量,于是就想出一个方法:将这堆货箱分别从正面、左面、上面所看到的平面图形画了出来,如图所示,你能根据这些平面图形帮他清点一下箱子的数量吗?这些正方体货箱的个数为( )