题目内容
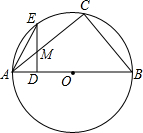 如图,AB是⊙O的直径,点C、E在
如图,AB是⊙O的直径,点C、E在 |
| AB |
(1)求证:点E是
 |
| AC |
(2)判断OD和BC之间的数量关系,并说明理由.
考点:圆周角定理,全等三角形的判定与性质
专题:
分析:(1)延长ED交⊙O于点F,由DE⊥AB,AB是⊙O的直径,根据垂径定理可得AE=AF,由AM=EM,得出∠MAE=∠MEA,那么AF=CE,等量代换得到AE=CE,根据圆心角、弧、弦的关系得出点E是
的中点;
(2)连接OE,交AC于H,由垂径定理的推论得出OH⊥AC,点H为AC中点,根据三角形中位线定理得到OH=
BC.由OA=OE,得出∠OAE=∠OEA,那么∠OAH=∠OED,利用AAS证明△OAH≌△OED,得出OD=OH,等量代换得到OD=
BC.
 |
| AC |
(2)连接OE,交AC于H,由垂径定理的推论得出OH⊥AC,点H为AC中点,根据三角形中位线定理得到OH=
| 1 |
| 2 |
| 1 |
| 2 |
解答: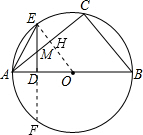 (1)证明:如图,延长ED交⊙O于点F,
(1)证明:如图,延长ED交⊙O于点F,
∵DE⊥AB,AB是⊙O的直径,
∴AE=AF.
∵AM=EM,
∴∠MAE=∠MEA,
∴AF=CE,
∴AE=CE,
即点E是
的中点;
(2)解:OD=
BC.理由如下:
连接OE,交AC于H,
∵点E是
的中点,
∴OH⊥AC,点H为AC中点,
∴OH=
BC.
∵OA=OE,
∴∠OAE=∠OEA,
∴∠OAH=∠OED.
在△OAH与△OED中,
,
∴△OAH≌△OED(AAS),
∴OD=OH,
∴OD=
BC.
 (1)证明:如图,延长ED交⊙O于点F,
(1)证明:如图,延长ED交⊙O于点F,∵DE⊥AB,AB是⊙O的直径,
∴AE=AF.
∵AM=EM,
∴∠MAE=∠MEA,
∴AF=CE,
∴AE=CE,
即点E是
 |
| AC |
(2)解:OD=
| 1 |
| 2 |
连接OE,交AC于H,
∵点E是
 |
| AC |
∴OH⊥AC,点H为AC中点,
∴OH=
| 1 |
| 2 |
∵OA=OE,
∴∠OAE=∠OEA,
∴∠OAH=∠OED.
在△OAH与△OED中,
|
∴△OAH≌△OED(AAS),
∴OD=OH,
∴OD=
| 1 |
| 2 |
点评:本题考查了垂径定理及其推论,等腰三角形的性质,圆心角、弧、弦的关系,全等三角形的判定与性质,三角形中位线定理,难度适中.准确作出辅助线是解题的关键.

练习册系列答案
相关题目
某种长途电话的收费方式如下,按通电话的第一分钟收费m元,之后的每一分钟收费n元,如果某人打长途电话按收费10元钱,则此人打长途电话的时间为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
在同一坐标系中,函数y=kx与y=
x-k的图象大致是( )
| 4 |
| 5 |
A、 |
B、 |
C、 |
D、 |
已知a>b,则下列不等式不能成立的是( )
| A、a-3>b-3 | ||||
| B、-2a>-2b | ||||
C、
| ||||
| D、-a<-b |
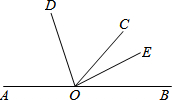 如图,∠AOB=180°,OD、OE分别是∠AOC和∠BOC的平分线,则∠AOD互余的角是( )
如图,∠AOB=180°,OD、OE分别是∠AOC和∠BOC的平分线,则∠AOD互余的角是( )| A、∠DOC |
| B、∠COE |
| C、∠COE与∠EOB |
| D、∠EOB |
 如图,是一个正方体的表面展开图,则原正方体中与“建”字所在的面相对的面上标的字是( )
如图,是一个正方体的表面展开图,则原正方体中与“建”字所在的面相对的面上标的字是( )| A、美 | B、丽 | C、重 | D、庆 |