题目内容
设x1、x2是方程2x2-4mx+2m2+3m-2=0的两个实数根,当m= 时,x12+x22有最小值,最小值是 .
考点:根与系数的关系,二次函数的最值
专题:
分析:由根与系数的关系知x12+x22是关于m的二次函数,是否是在抛物线的顶点处取得最小值,就要看自变量m的取值范围,从判别式入手.
解答:解:∵x1、x2是方程2x2-4mx+2m2+3m-2=0的两个实根,
∴△=(-4m)2-4×2×(2m2+3m-2)≥0,可得m≤
,
又x1+x2=2m,x1x2=
,
∴x12+x22=2(m-
)2+
=2(
-m)2+
,
∵m≤
,
∴
-m>0,
∴当m=
时,x12+x22取得最小值为2(
-
)2+
=
.
故答案为
,
.
∴△=(-4m)2-4×2×(2m2+3m-2)≥0,可得m≤
| 2 |
| 3 |
又x1+x2=2m,x1x2=
| 2m2+3m-2 |
| 2 |
∴x12+x22=2(m-
| 3 |
| 4 |
| 7 |
| 8 |
| 3 |
| 4 |
| 7 |
| 8 |
∵m≤
| 2 |
| 3 |
∴
| 3 |
| 4 |
∴当m=
| 2 |
| 3 |
| 3 |
| 4 |
| 2 |
| 3 |
| 7 |
| 8 |
| 8 |
| 9 |
故答案为
| 2 |
| 3 |
| 8 |
| 9 |
点评:本题考查了根与系数的关系,二次函数最值问题及根的判别式,难度较大,关键掌握:当抛物线的顶点在该区间内,顶点的纵坐标就是函数的最值,当抛物线的顶点不在该区间内,二次函数的最值在区间内两端点处取得.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
在同一坐标系中,函数y=kx与y=
x-k的图象大致是( )
| 4 |
| 5 |
A、 |
B、 |
C、 |
D、 |
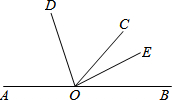 如图,∠AOB=180°,OD、OE分别是∠AOC和∠BOC的平分线,则∠AOD互余的角是( )
如图,∠AOB=180°,OD、OE分别是∠AOC和∠BOC的平分线,则∠AOD互余的角是( )| A、∠DOC |
| B、∠COE |
| C、∠COE与∠EOB |
| D、∠EOB |
 如图,是一个正方体的表面展开图,则原正方体中与“建”字所在的面相对的面上标的字是( )
如图,是一个正方体的表面展开图,则原正方体中与“建”字所在的面相对的面上标的字是( )| A、美 | B、丽 | C、重 | D、庆 |
在-0.202002,
,
,-
,
,0中,无理数的个数是( )
| 11 |
| 22 |
| 7 |
| π |
| 2 |
| 4 |
| A、1个 | B、2个 | C、3个 | D、4个 |