Question

2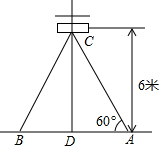．如图，在电线杆离地面6米高的C处向地面拉缆绳，缆绳和地面成60°角，那么缆绳AC的长等于4$\sqrt{3}$．（保留根号）

Answer 1

分析 在Rt△ACD中，设AD=x，则AC=2x，利用勾股定理列出方程即可解决问题．

解答 解：在Rt△ACD中，∵∠ADC=90°，CD=6，∠CAD=60°，
∴∠ACD=30°，
∴AC=2AD，设AD=x，则AC=2x，
∵（2x）²=x²+6²，
∴x=±2$\sqrt{3}$，
∵x＞0，
∴x=2$\sqrt{3}$，
∴AC=4$\sqrt{3}$．
故答案为4$\sqrt{3}$

点评 本题考查解直角三角形的应用，解题关键是学会设未知数，构建方程解决问题，属于中考常考题型．