题目内容
5. 如图,正方形网格中的格点△ABC,已知小方格边长为1.
如图,正方形网格中的格点△ABC,已知小方格边长为1.(1)求△ABC的面积;
(1)判断△ABC是哪一种特殊三角形?并说明理由.
分析 (1)用大长方形的面积减去三个小三角形的面积,即可求出△ABC的面积.
(2)根据勾股定理求得△ABC各边的长,再利用勾股定理的逆定理进行判定,从而得到其形状.
解答  解:(1)△ABC的面积=4×8-1×8÷2-2×3÷2-6×4÷2=13,
解:(1)△ABC的面积=4×8-1×8÷2-2×3÷2-6×4÷2=13,
故△ABC的面积为13;
(2)△ABC是直角三角形.
∵正方形小方格边长为1
∴AC2=12+82=65,AB2=32+22=13,BC2=62+42=52,
∵在△ABC中,AB2+BC2=13+52=65,AC2=65,
∴AB2+BC2=AC2,
∴网格中的△ABC是直角三角形.
点评 本题主要考查勾股定理和勾股定理的逆定理的应用,要判断一个角是不是直角,先要构造出三角形,然后知道三条边的大小,用较小的两条边的平方和与最大的边的平方比较,如果相等,则三角形为直角三角形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
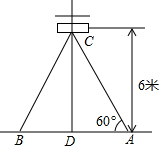 如图,在电线杆离地面6米高的C处向地面拉缆绳,缆绳和地面成60°角,那么缆绳AC的长等于4$\sqrt{3}$.(保留根号)
如图,在电线杆离地面6米高的C处向地面拉缆绳,缆绳和地面成60°角,那么缆绳AC的长等于4$\sqrt{3}$.(保留根号)