题目内容
14. 东西走向笔直的高速公路AB一侧有服务区,服务区内有加油站C,一汽车加油时需要从东面沿着与高速公路成30°角的方向开200m,再在服务区内自西向东行驶100m到加油站加油,然后沿着与高速公路成40°角的方向驶回高速公路.求:该汽车加油过程比不加油直接在高速公路上开多行驶的路程(精确到1m,参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,$\sqrt{3}≈1.73$).
东西走向笔直的高速公路AB一侧有服务区,服务区内有加油站C,一汽车加油时需要从东面沿着与高速公路成30°角的方向开200m,再在服务区内自西向东行驶100m到加油站加油,然后沿着与高速公路成40°角的方向驶回高速公路.求:该汽车加油过程比不加油直接在高速公路上开多行驶的路程(精确到1m,参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,$\sqrt{3}≈1.73$).
分析 先将梯形分割成直角三角形和矩形,利用锐角三角函数求出AF,BC,AB,即可.
解答 解:过点C作CE⊥AB,过点D作DF⊥AB.
∴四边形CDFE是矩形,
∴CE=DF,EF=CD=100m,
在Rt△ADF中,DF=ADsin30°=100,
AF=ADcos30°≈173,
在Rt△BCE中,BC=$\frac{CE}{sin40°}$≈156,
BE=$\frac{CE}{tan40°}$≈119,
∴AB=AF+EF+BE=392m,
AD+CD+BC=456m,
∴AD+CD+BC-AB=64m,
答:汽车进加油站加油比不加油多行驶了大约64m.
点评 此题是直角三角形的应用,主要考查了梯形的性质,锐角三角形函数,解本题的根据是梯形辅助线的作法,要熟记梯形的几种辅助线的作法是解梯形题目的关键.

练习册系列答案
相关题目
19. 如图,点E在正方形ABCD外,∠AEB=90°,若AE=6,BE=8,则正方形ABCD的面积是( )
如图,点E在正方形ABCD外,∠AEB=90°,若AE=6,BE=8,则正方形ABCD的面积是( )
 如图,点E在正方形ABCD外,∠AEB=90°,若AE=6,BE=8,则正方形ABCD的面积是( )
如图,点E在正方形ABCD外,∠AEB=90°,若AE=6,BE=8,则正方形ABCD的面积是( )| A. | 48 | B. | 24 | C. | 10 | D. | 100 |
 如图,已知,在Rt△ABC中,∠ABC=90°,BD⊥AC于D.
如图,已知,在Rt△ABC中,∠ABC=90°,BD⊥AC于D.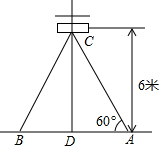 如图,在电线杆离地面6米高的C处向地面拉缆绳,缆绳和地面成60°角,那么缆绳AC的长等于4$\sqrt{3}$.(保留根号)
如图,在电线杆离地面6米高的C处向地面拉缆绳,缆绳和地面成60°角,那么缆绳AC的长等于4$\sqrt{3}$.(保留根号) 如图,△ABC中,AB=AC,以AB为直径作⊙O,分别交AC,BC于点D,E.
如图,△ABC中,AB=AC,以AB为直径作⊙O,分别交AC,BC于点D,E. 如图,已知直线y=$\frac{1}{2}$x与双曲线y=$\frac{k}{x}$(k>0)交于A,B两点,且点A的横坐标为4,
如图,已知直线y=$\frac{1}{2}$x与双曲线y=$\frac{k}{x}$(k>0)交于A,B两点,且点A的横坐标为4,