题目内容
17. 已知抛物线的解析式为y=-$\frac{1}{2}$x2+x+$\frac{5}{2}$.
已知抛物线的解析式为y=-$\frac{1}{2}$x2+x+$\frac{5}{2}$.(1)求出抛物线的顶点坐标;
(2)在平面直角坐标系中画出抛物线的图象;
(3)点A(a,b)是抛物线上一点,直接写出当a取何值时b>$\frac{5}{2}$.
分析 (1)配方成二次函数顶点式即可得顶点坐标;
(2)描点、连线即可得函数图象;
(3)根据函数图象即可得.
解答 解:(1)y=-$\frac{1}{2}$x2+x+$\frac{5}{2}$
=-$\frac{1}{2}$(x2-2x)+$\frac{5}{2}$,
=-$\frac{1}{2}$(x-1)2+3,
∴顶点坐标为(1,3);
(2)如图:
(3)由(2)中函数图象可知,当0<a<2时,b>$\frac{5}{2}$.
点评 此题主要考查了二次函数的性质以及配方法求二次函数的顶点坐标,利用数形结合得出图象在y>$\frac{5}{2}$时x的范围是解题关键.

练习册系列答案
相关题目
12. 如图所示,弹簧不挂重物时的长度是( )
如图所示,弹簧不挂重物时的长度是( )
 如图所示,弹簧不挂重物时的长度是( )
如图所示,弹簧不挂重物时的长度是( )| A. | 9cm | B. | 10cm | C. | 10.5cm | D. | 11cm |
 如图,已知,在Rt△ABC中,∠ABC=90°,BD⊥AC于D.
如图,已知,在Rt△ABC中,∠ABC=90°,BD⊥AC于D.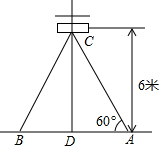 如图,在电线杆离地面6米高的C处向地面拉缆绳,缆绳和地面成60°角,那么缆绳AC的长等于4$\sqrt{3}$.(保留根号)
如图,在电线杆离地面6米高的C处向地面拉缆绳,缆绳和地面成60°角,那么缆绳AC的长等于4$\sqrt{3}$.(保留根号) 如图,△ABC中,AB=AC,以AB为直径作⊙O,分别交AC,BC于点D,E.
如图,△ABC中,AB=AC,以AB为直径作⊙O,分别交AC,BC于点D,E. 如图,已知直线y=$\frac{1}{2}$x与双曲线y=$\frac{k}{x}$(k>0)交于A,B两点,且点A的横坐标为4,
如图,已知直线y=$\frac{1}{2}$x与双曲线y=$\frac{k}{x}$(k>0)交于A,B两点,且点A的横坐标为4,