题目内容
19.在一次女子排球比赛中,甲、乙两队参赛选手的年龄(单位:岁)如下:甲队:26,25,28,28,24,28,26,28,27,29;
乙队:28,27,25,28,27,26,28,27,27,26.
(1)两队参赛选手的平均年龄分别是多少?
(2)利用标准差比较说明两队参赛选手年龄波动的情况如何.
分析 (1)根据平均数的计算公式分别计算甲乙两队参赛选手的平均年龄;
(2)先利用方差公式计算出甲乙两队的方差,再计算它们的标准差,然后根据标准差的意义判断两队参赛选手年龄波动的情况如何.
解答 解:(1)甲队选手的平均年龄为$\frac{1}{10}$(26+25+28+28+24+28+26+28+27+29)=26.9(岁);
乙队选手的平均年龄为$\frac{1}{10}$(28+27+25+28+27+26+28+27+27+26)=26.9(岁);
(2)甲队的方差=$\frac{1}{10}$[(26-26.9)2+(25-26.9)2+(28-26.9)2+(28-26.9)2+(24-26.9)2+(28-26.9)2+(26-26.9)2+(28-26.9)2+(27-26.9)2+(29-26.9)2]=2.29,
乙队的方差=$\frac{1}{10}$[(28-26.9)2+(27-26.9)2+(58-26.9)2+(28-26.9)2+(27-26.9)2+(26-26.9)2+(28-26.9)2+(27-26.9)2+(27-26.9)2+(26-26.9)2]=0.89,
甲队的标准差=$\sqrt{2.29}$≈1.51,乙队的标准差=$\sqrt{0.89}$≈0.943,
因为甲队的标准差大于乙队的标准差,
所以乙对参赛选手年龄波动较小.
点评 本题考查了标准差:样本的标准差就是样本方差的算术平方根;标准差是反应一组数据离散程度最常用的一种量化形式,是表示精密确的最要指标.标准差越大,则平均值的离散程度越大,稳定性也越小;反之,则它与其平均值的离散程度越小,稳定性越好.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
9.某单位欲招聘管理人员一名,对甲、乙、丙三名候选人进行了笔试和面试两项测试,三人的成绩如表:已知甲、乙、丙三名候选人的民主得分依次是25分,40分,35分.根据需要,单位将笔试、面试、民主评议三项测试得分按4:3:3的比例确定个人成绩,那么谁将被录用?
| 测试项目 | 测试成绩/分 | ||
| 甲 | 乙 | 丙 | |
| 笔试 | 80 | 90 | 90 |
| 面试 | 100 | 70 | 80 |
8.若kb<0,则直线y=kx+b一定通过( )
| A. | 第一、二象限 | B. | 第二、三象限 | C. | 第三、四象限 | D. | 第四、一象限 |
9.1的平方根是( )
| A. | 0 | B. | 1 | C. | ±1 | D. | -1 |
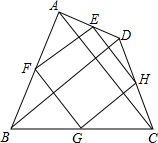 四边形ABCD中,点E、F、G、H分别是边AD、AB、BC、CD的中点
四边形ABCD中,点E、F、G、H分别是边AD、AB、BC、CD的中点 如图,矩形ABCD中,AB=$\frac{1}{n}$AD(n为大于1的整数),作对角线BD的垂直平分线分别交AD,BC于点E,F,EF与BD的交点为O,连接BE和DF.
如图,矩形ABCD中,AB=$\frac{1}{n}$AD(n为大于1的整数),作对角线BD的垂直平分线分别交AD,BC于点E,F,EF与BD的交点为O,连接BE和DF.
