题目内容
19．抛物线y=x2-4与x轴交于B，C两点，顶点为A，则△ABC的面积为（ ）| A． | 16 | B． | 8 | C． | 4 | D． | 2 |
分析 首先求得B、C的坐标，则BC的长即可求得，然后求得A的坐标，根据三角形的面积公式即可求解．
解答 解：在y=x2-4中，令y=0，则x2-4=0，
解得x1=-2，x2=2，
则B和C的坐标是（-2，0）和（2，0），BC=4．
抛物线y=x2-4的顶点是（0，-4），
则S△ABC=$\frac{1}{2}$×4×4=8．
故选B．
点评 本题考查了二次函数与x轴的交点，求与x轴的交点时，令y=0，即可得到关于x的方程，解方程求得交点的横坐标．
练习册系列答案
相关题目
如图，在△ABC中，∠A=60°，BC=10，BO平分∠ABC，CO平分∠ACB，MN经过点O与AB，AC相交于点M，N，且MN∥BC，△AMN的周长为18．
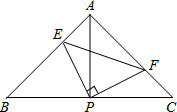如图，已知△ABC中，AB=AC，∠BAC=90°，直角∠EPF的顶点P是BC中点，两边PE、PF分别交AB、AC于点E、F，给出以下四个结论：
如图，四边形ABCD中，AB=DC，∠A=∠D，M、N分别是AD、BC的中点，E、F分别是BM、CM的中点，求证：四边形MENF是菱形．
已知：实数a，b在数轴上的位置如图所示，化简：$\sqrt{（a+1）^{2}}$+2$\sqrt{（b-1）^{2}}$-|a-b|．