题目内容
10.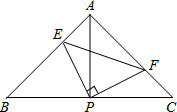 如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE、PF分别交AB、AC于点E、F,给出以下四个结论:
如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE、PF分别交AB、AC于点E、F,给出以下四个结论:(1)△EPF是等腰直角三角形;(2)S四边形AEPF=$\frac{1}{2}$S△ABC;(3)2EF≥BC;(4)BE2+CF2=EF2,
当∠EPF在△ABC内绕顶点P旋转时(点E不与A、B重合),上述结论中始终正确的有(1)(2)(3)(4)(填序号)
分析 通过证明△AFP≌△BEP就可以得出AF=BE,EP=PF,得出AE=CF,得出△EPF是等腰直角三角形,由S四边形AEPF=S△APE+S△APF.就可以得出S四边形AEPF=S△CPF+S△APF,就可以得出结论,由AF=BE,AE=CF得出EF2=BE2+CF2;求得当EP⊥AB时,EP取最小值,此时EP=$\frac{1}{2}$AB,则EF最小值=$\frac{\sqrt{2}}{2}$AB=$\frac{1}{2}$BC,进一步得出结论.
解答 解:∵AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC的中点,
∴∠B=∠PAF=45°,BP=AP,
∵∠APE+∠BPE=90°,∠APE+∠APF=90°,
∴∠BPE=∠APF.
在△BPE和△APF中,
$\left\{\begin{array}{l}{∠B=∠PAF}\\{BP=AP}\\{∠BPE=∠APF}\end{array}\right.$,
∴△AFP≌△BEP(ASA),
∴BE=AF,PE=PF,
故(1)△EPF是等腰直角三角形正确;
∵EPF=90°,
在Rt△EPF中,由勾股定理,得EF2=PE2+PF2,
∴EF2=BE2+CF2.故(4)正确;
∵S四边形AEPF=S△APE+S△APF.
∴S四边形AEPF=S△CPF+S△APF=S△FAE=$\frac{1}{2}$S△ABC.故(2)正确.
由(1)知,△EPF是等腰直角三角形,则EF=$\sqrt{2}$EP.
当EP⊥AB时,EP取最小值,此时EP=$\frac{1}{2}$AB,则EF最小值=$\frac{\sqrt{2}}{2}$AB=$\frac{1}{2}$BC,
则2EF≥BC.故(3)正确;
故答案为:(1)(2)(3)(4).
点评 本题考查了等腰直角三角形的性质的运用,全等三角形的判定及性质的运用,中位线的性质的运用,等腰直角三角形的判定定理的运用,三角形面积公式的运用,解答时灵活运用等腰直角三角形的性质求解是关键.

 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案| A. | 16 | B. | 8 | C. | 4 | D. | 2 |
 在下面五幅图案中,哪一幅图案可以通过平移如图所示图案得到( )
在下面五幅图案中,哪一幅图案可以通过平移如图所示图案得到( )



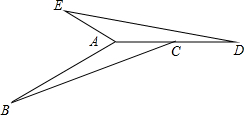 在△ABC中,∠B+∠ACB=30°,AB=4,△ABC逆时针旋转一定角度后与△ADE重合,且点C恰好成为AD中点,如图
在△ABC中,∠B+∠ACB=30°,AB=4,△ABC逆时针旋转一定角度后与△ADE重合,且点C恰好成为AD中点,如图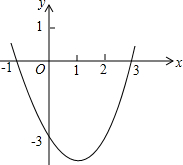 二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象解答下列问题:
二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象解答下列问题: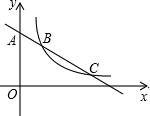 如图,直线y=一$\frac{{\sqrt{3}}}{3}$x+b与y轴交于点A,与双曲线y=$\frac{k}{x}$在第一象限交于B、C两点,且AB•AC=12,则k值为3$\sqrt{3}$.
如图,直线y=一$\frac{{\sqrt{3}}}{3}$x+b与y轴交于点A,与双曲线y=$\frac{k}{x}$在第一象限交于B、C两点,且AB•AC=12,则k值为3$\sqrt{3}$.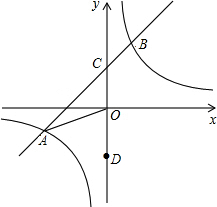 如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函数y=$\frac{m}{x}$(m≠0)的图象交于一、三象限内的A、B两点,与y轴交于C点,点B的坐标为(3,n).线段AO=13,D为y轴上一点,且sin∠AOD=$\frac{5}{13}$.
如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函数y=$\frac{m}{x}$(m≠0)的图象交于一、三象限内的A、B两点,与y轴交于C点,点B的坐标为(3,n).线段AO=13,D为y轴上一点,且sin∠AOD=$\frac{5}{13}$.