题目内容
14. 已知:实数a,b在数轴上的位置如图所示,化简:$\sqrt{(a+1)^{2}}$+2$\sqrt{(b-1)^{2}}$-|a-b|.
已知:实数a,b在数轴上的位置如图所示,化简:$\sqrt{(a+1)^{2}}$+2$\sqrt{(b-1)^{2}}$-|a-b|.
分析 根据数轴得出a-b<0,b-1>0,a+1<0,进而化简求出即可.
解答 解:如图所示:
a-b<0,b-1>0,a+1<0,
则:$\sqrt{(a+1)^{2}}$+2$\sqrt{(b-1)^{2}}$-|a-b|
=-(a+1)-2(b-1)+(a-b)
=-a-1-2b+2+a-b
=-3b+1.
点评 此题主要考查了实数与数轴以及二次根式和绝对值的性质,正确化简二次根式是解题关键.

练习册系列答案
相关题目
9. 如图,在线段AE上依次有B、C、D三点,则图中共有线段( )
如图,在线段AE上依次有B、C、D三点,则图中共有线段( )
 如图,在线段AE上依次有B、C、D三点,则图中共有线段( )
如图,在线段AE上依次有B、C、D三点,则图中共有线段( )| A. | 1条 | B. | 4条 | C. | 8条 | D. | 10条 |
19.抛物线y=x2-4与x轴交于B,C两点,顶点为A,则△ABC的面积为( )
| A. | 16 | B. | 8 | C. | 4 | D. | 2 |
6.如果点A(-2,a),B(b,1)是反比例函数y=-$\frac{6}{x}$图象上的两点,那么a,b的值分别是( )
| A. | 3,6 | B. | -3,6 | C. | 3,-6 | D. | -3,-6 |
 在已给图形的基础上画图,使之成为图形,并且满足第一幅图只有一条对称轴,第二幅图只有两条对称轴.
在已给图形的基础上画图,使之成为图形,并且满足第一幅图只有一条对称轴,第二幅图只有两条对称轴.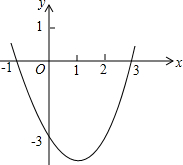 二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象解答下列问题:
二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象解答下列问题: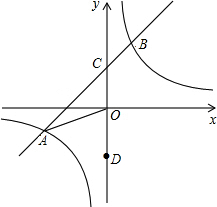 如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函数y=$\frac{m}{x}$(m≠0)的图象交于一、三象限内的A、B两点,与y轴交于C点,点B的坐标为(3,n).线段AO=13,D为y轴上一点,且sin∠AOD=$\frac{5}{13}$.
如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函数y=$\frac{m}{x}$(m≠0)的图象交于一、三象限内的A、B两点,与y轴交于C点,点B的坐标为(3,n).线段AO=13,D为y轴上一点,且sin∠AOD=$\frac{5}{13}$. 已知:如图,点E在△ABC的边BA延长线上,AD∥BC,∠B=∠C.求证:AD平分∠EAC.
已知:如图,点E在△ABC的边BA延长线上,AD∥BC,∠B=∠C.求证:AD平分∠EAC.