题目内容
18. 如图,矩形ABCD的对角线AC,BD相交于点O,以下说法不一定正确的是( )
如图,矩形ABCD的对角线AC,BD相交于点O,以下说法不一定正确的是( )| A. | ∠ABC=90° | B. | AC=BD | C. | ∠OAB=∠OBA | D. | OA=AD |
分析 A、利用矩形的四个角是直角得结论;
B、利用矩形的对角线相等得结论;
C、利用矩形对角线相等且平分,再由等边对等角得结论;
D、当∠DAO=60°时才成立.
解答 解:A、根据矩形的四个角是直角得:∠ABC=90°,所以选项A说法正确;
B、根据矩形的对角线相等得:AC=BD,所以选项B说法正确;
C、∵四边形ABCD是矩形,
∴AC=BD,OA=$\frac{1}{2}$AC,OB=$\frac{1}{2}$BD,
∴OA=OB,
∴∠OAB=∠OBA,
所以选项C说法正确;
D、同理得:OD=OA,
当∠DAO=60°时,△ADO是等边三角形,
即OA=AD,
但本题∠DAO的度数未知,所以选项D说法不一定正确;
故选D.
点评 本题考查了矩形的性质,熟练掌握矩形的性质是关键:①矩形的四个角都是直角;②矩形的对角线相等且平分.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
13.已知等腰三角形一边长等于4,一边长等于9,它的周长是( )
| A. | 17或22 | B. | 22 | C. | 17 | D. | 13 |
10.分式$\frac{1}{{x}^{2}-x}$,$\frac{1}{{x}^{2}+x}$的最简公分母是( )
| A. | (x+1)(x-1) | B. | x(x+1)(x-1) | C. | x2(x+1)(x-1) | D. | x(x-1)2 |
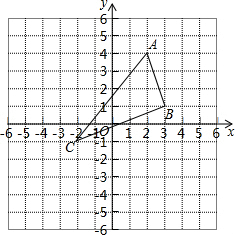 如图,在平面直角坐标系中,A(2,4),B(3,1),C(-2,-1).
如图,在平面直角坐标系中,A(2,4),B(3,1),C(-2,-1).