题目内容
8.若关于x的不等式组$\left\{\begin{array}{l}{x<2(x-a)}\\{x-1≤\frac{2}{3}x}\end{array}\right.$恰好有3个整数解.(1)写出该不等式组的整数解.
(2)求a的取值范围.
分析 (1)先求出每个不等式的解集,求出不等式组的解集,再根据不等式组有且只有三个整数解求出整数解.
(2)根据整数解和不等式组的解集,即可求得a的取值范围
解答 解:解不等式x<2(x-a),得:x>2a,
解不等式x-1≤$\frac{2}{3}$x,得:x≤3,
∴不等式组的解集:2a<x≤3
∵不等式组的整数解共有3个:
∴该不等式组的整数解为1,2,3;
(2)∵不等式组的解集:2a<x≤3,整数解为1,2,3;
∴0≤2a<1,
∴0≤a<$\frac{1}{2}$.
点评 此题考查了不等式组的整数解,关键是根据不等式组的整数解求出取值范围,用到的知识点是一元一次不等式的解法.

练习册系列答案
相关题目
18. 如图,矩形ABCD的对角线AC,BD相交于点O,以下说法不一定正确的是( )
如图,矩形ABCD的对角线AC,BD相交于点O,以下说法不一定正确的是( )
 如图,矩形ABCD的对角线AC,BD相交于点O,以下说法不一定正确的是( )
如图,矩形ABCD的对角线AC,BD相交于点O,以下说法不一定正确的是( )| A. | ∠ABC=90° | B. | AC=BD | C. | ∠OAB=∠OBA | D. | OA=AD |
19.我们学习了怎样作一个角等于已知角,小迪发现实际的作图过程就是作一个三角形与原来的三角形全等.那么,你能说出它运用的是哪个判定三角形全等的方法呢?( )
| A. | AAS | B. | ASA | C. | SSS | D. | SAS |
13.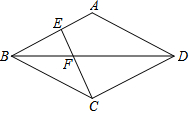 如图,菱形ABCD中,BD为ABCD的对角线,且CE⊥AB,交BD于点F,BD=8,AB=5,则CE的值是( )
如图,菱形ABCD中,BD为ABCD的对角线,且CE⊥AB,交BD于点F,BD=8,AB=5,则CE的值是( )
 如图,菱形ABCD中,BD为ABCD的对角线,且CE⊥AB,交BD于点F,BD=8,AB=5,则CE的值是( )
如图,菱形ABCD中,BD为ABCD的对角线,且CE⊥AB,交BD于点F,BD=8,AB=5,则CE的值是( )| A. | $\frac{12}{5}$ | B. | $\frac{24}{5}$ | C. | $\frac{48}{5}$ | D. | $\frac{8}{5}$ |
 如图,四边形ABCD内接于圆,延长AD、BC相交于点E,点F是BD的延长线上的点,且AB=AC.
如图,四边形ABCD内接于圆,延长AD、BC相交于点E,点F是BD的延长线上的点,且AB=AC.