题目内容
13.将两个全等的直角三角形ABC和DEC按图1放置,点E在AB上,∠ACB=∠DCE=90°,∠BAC=∠EDC=30°.(1)求证:AE=BE;
(2)如图2,△ABC不动,将△DEC绕点C旋转,猜想△AEC和△DBC面积的大小关系,并证明你的猜想.

分析 (1)先判定△CBE为等边三角形得到∠BCE=60°,则∠ACE=30°,所以∠ACE=∠A,然后根据等腰三角形的判定定理即可得到结论;
(2)作AN⊥CE于N,DM⊥BC于M,如图,证明△ANC≌△DMC得到AN=DM,然后根据三角形面积公式可判断S△AEC=S△DBC.
解答 (1)证明:∵∠ACB=90°,∠BAC=30°.
∴∠B=60°,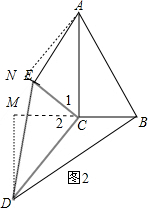
∵△ABC和△DCE全等,
∴CE=CB,
∴△CBE为等边三角形,
∴∠BCE=60°,
∴∠ACE=30°,
∴∠ACE=∠A,
∴AE=BE;
(2)解:△AEC和△DBC面积相等.理由如下:
作AN⊥CE于N,DM⊥BC于M,如图,
∴CA=CD,
∵∠ACB=∠DCE=90°,
即∠1+∠MCN=90°,∠2+∠MCN=90°,
∴∠1=∠2,
在△ANC和△DMC中
$\left\{\begin{array}{l}{∠ANC=∠DMC}\\{∠1=∠2}\\{AC=DC}\end{array}\right.$,
∴△ANC≌△DMC(AAS),
∴AN=DM,
而S△AEC=$\frac{1}{2}$•CE•AN,S△DBC=$\frac{1}{2}$•BC•DM,
S△AEC=S△DBC.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了全等三角形的判定与性质和三角形面积公式.

练习册系列答案
相关题目
5.如果点(-2,3)在反比例函数y=$\frac{k}{x}$(k≠0的常数)的图象上,那么对于反比例函数y=$\frac{k}{x}$下列说法正确的是( )
| A. | 在每一象限内,y随x的增大而增大 | B. | 在每一象限内,y随x的增大而减小 | ||
| C. | y恒为正值 | D. | y恒为负值 |
3.已知图中的两个三角形全等,则∠1等于( )


| A. | 52° | B. | 60° | C. | 68° | D. | 70° |
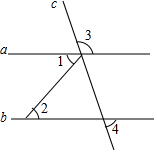 如图,若∠1=40°30′,∠2=40°30′,∠3=120°,则∠4=60°.
如图,若∠1=40°30′,∠2=40°30′,∠3=120°,则∠4=60°. 如图,在△ABC中,∠ABC=2∠C,∠BAC的平分线AD交BC于D,过B作BE⊥AD交AD于F,交AC于E.
如图,在△ABC中,∠ABC=2∠C,∠BAC的平分线AD交BC于D,过B作BE⊥AD交AD于F,交AC于E. 如图,已知A(-4,-$\frac{1}{2}$),B(-1,-2)是一次函数y=kx+b与反比例函数y=$\frac{m}{x}$(m>0,x<0)图象的两个交点,AC⊥x轴于C,BD⊥y轴于D.
如图,已知A(-4,-$\frac{1}{2}$),B(-1,-2)是一次函数y=kx+b与反比例函数y=$\frac{m}{x}$(m>0,x<0)图象的两个交点,AC⊥x轴于C,BD⊥y轴于D.