题目内容
17．若数轴上表示数x的点在原点的左边，则化简|x|+$\sqrt{{x}^{2}}$的结果是（ ）| A． | 2x | B． | -2x | C． | 0 | D． | x |
分析 由题意知x＜0，可得|x|=$\sqrt{{x}^{2}}$=-x，化简即可得．
解答 解：∵数轴上表示数x的点在原点的左边，
∴x＜0，
∴|x|+$\sqrt{{x}^{2}}$=-x-x=-2x，
故选：B．
点评 本题主要考查二次根式的性质与化简、实数与数轴，确定x的取值范围是前提，正确的去绝对值号和根号是关键．
练习册系列答案
相关题目
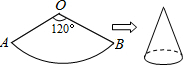如图，一个扇形铁皮OAB，已知OA=12cm，∠AOB=120°，小华将OA、OB合拢制成了一个圆锥形烟囱帽（接缝处忽略不计），则烟囱帽的高为8$\sqrt{2}$cm．
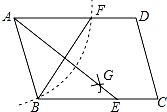如图，在平行四边形ABCD中，以A为圆心，AB为半径画弧，交AD于F，再分别以B、F为圆心，大于$\frac{1}{2}$BF的长为半径画弧，两弧相交于点G，若BF=6，AB=5，则AE的长为（ ）