题目内容
14.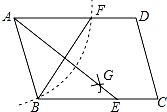 如图,在平行四边形ABCD中,以A为圆心,AB为半径画弧,交AD于F,再分别以B、F为圆心,大于$\frac{1}{2}$BF的长为半径画弧,两弧相交于点G,若BF=6,AB=5,则AE的长为( )
如图,在平行四边形ABCD中,以A为圆心,AB为半径画弧,交AD于F,再分别以B、F为圆心,大于$\frac{1}{2}$BF的长为半径画弧,两弧相交于点G,若BF=6,AB=5,则AE的长为( )| A. | 11 | B. | 6 | C. | 8 | D. | 10 |
分析 连接EF,根据题意得出AE垂直平分BF,AF=AB=5,得出OB=OF=3,∠BAE=∠FAE,由勾股定理求出OA,再证出BE=AB=AF,得出四边形ABEF是平行四边形,由平行四边形的性质得出OA=OE=$\frac{1}{2}$AE,即可得出结果.
解答 解:连接EF,如图所示: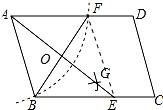
根据题意得:AE垂直平分BF,AF=AB=5,
∴∠AOF=90°,OB=OF=3,∠BAE=∠FAE,
∴OA=$\sqrt{A{F}^{2}-O{F}^{2}}$=4,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠FAE=∠AEB,
∴∠BAE=∠AEB,
∴BE=AB=AF,
∴四边形ABEF是平行四边形,
∴OA=OE=$\frac{1}{2}$AE,
∴AE=2OA=8;
故选:C.
点评 本题考查了平行四边形的性质与判定、垂直平分线的性质、勾股定理;熟练掌握平行四边形的性质,证明四边形ABEF是平行四边形是解决问题的关键.

练习册系列答案
相关题目
5.若顺次连接四边形的各边中点所得的四边形是菱形,则该四边形一定是( )
| A. | 矩形 | B. | 菱形 | ||
| C. | 对角线相等的四边形 | D. | 对角线互相垂直的四边形 |
9.若反比例函数y=$\frac{k}{x}$的图象经过点(-3,2),则反比例函数y=-$\frac{k}{x}$的图象在( )
| A. | 一、二象限 | B. | 三、四象限 | C. | 一、三象限 | D. | 二、四象限 |
17.若数轴上表示数x的点在原点的左边,则化简|x|+$\sqrt{{x}^{2}}$的结果是( )
| A. | 2x | B. | -2x | C. | 0 | D. | x |