题目内容
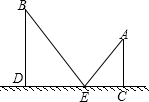 如图,在台球赛中,一球在点A处,要从A射出,经台球边挡板CD反射,击中球B.已知AC=10cm,BD=15cm,CD=xcm,EC=ycm,恰好能击中球B,求y关于x的函数解析式.
如图,在台球赛中,一球在点A处,要从A射出,经台球边挡板CD反射,击中球B.已知AC=10cm,BD=15cm,CD=xcm,EC=ycm,恰好能击中球B,求y关于x的函数解析式.考点:相似三角形的应用,函数关系式
专题:
分析:易得∠ACE=∠BDE=90°,利用入射角等于反射角可得∠BED=∠AEC,那么可得△ACE∽△BDE.利用相似三角形的对应边成比例可得y关于x的函数解析式.
解答:解:∵∠BED=∠AEC,∠BDE=∠ACE=90°,
∴△ACE∽△BDE.
∴
=
,
∵AC=10cm,BD=15cm,CD=xcm,EC=ycm,
∴
=
.
整理得:y=
x.
∴y关于x的函数解析式是y=
x.
∴△ACE∽△BDE.
∴
| BD |
| AC |
| DE |
| EC |
∵AC=10cm,BD=15cm,CD=xcm,EC=ycm,
∴
| 15 |
| 10 |
| x-y |
| y |
整理得:y=
| 2 |
| 5 |
∴y关于x的函数解析式是y=
| 2 |
| 5 |
点评:考查相似三角形的应用;用到的知识点为:两角对应相等的两三角形相似;相似三角形的对应边成比例.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
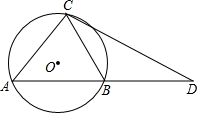 如图,A、C为⊙O上两点,DA交⊙O于点B,连接AC、BC,若∠DCB=∠A,直线CD与⊙O相切吗?证明你的结论.
如图,A、C为⊙O上两点,DA交⊙O于点B,连接AC、BC,若∠DCB=∠A,直线CD与⊙O相切吗?证明你的结论.