题目内容
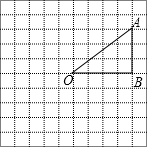 如图,方格纸中的每格都是边长为1的正方形,将△OAB(顶点都是正方形的顶点)绕点O按逆时针方向旋转90°得到△OA1B1.
如图,方格纸中的每格都是边长为1的正方形,将△OAB(顶点都是正方形的顶点)绕点O按逆时针方向旋转90°得到△OA1B1.(1)在所给的图形中画出△OA1B1;
(2)线段A1B的长为
考点:作图-旋转变换,扇形面积的计算
专题:
分析:(1)利用旋转的性质得出对应点B1,以及A1的位置进而得出答案;
(2)直接利用网格以及勾股定理得出线段A1B的长,再利用扇形面积公式得出即可.
(2)直接利用网格以及勾股定理得出线段A1B的长,再利用扇形面积公式得出即可.
解答: 解:(1)如图所示:△OA1B1即为所求;
解:(1)如图所示:△OA1B1即为所求;
(2)线段A1B的长为:
=
,
∵AO=
=5,∠AOA1=90°,
∴此过程中线段OA所扫过的图形的面积为:S扇形AOA1=
=
.
故答案为:
,
.
 解:(1)如图所示:△OA1B1即为所求;
解:(1)如图所示:△OA1B1即为所求;(2)线段A1B的长为:
| 72+42 |
| 65 |
∵AO=
| 42+32 |
∴此过程中线段OA所扫过的图形的面积为:S扇形AOA1=
| 90π×AO2 |
| 360 |
| 25π |
| 4 |
故答案为:
| 65 |
| 25π |
| 4 |
点评:此题主要考查了旋转变换以及扇形面积求法和勾股定理等知识,熟练利用勾股定理得出是解题关键.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
下列各式能用平方差公式计算的是( )
| A、(2a+b)(2b-a) | ||||
B、(-
| ||||
| C、(a+b)(a-2b) | ||||
| D、(2x-1)(-2x+1) |
 如图1是一张折叠椅子,图2是其侧面示意图,已知椅子折叠时长1.2米.椅子展开后最大张角∠CBD=37°,且BD=BC,AB:BG:GC=1:2:3,座面EF与地面平行,当展开角最大时,请解答下列问题:
如图1是一张折叠椅子,图2是其侧面示意图,已知椅子折叠时长1.2米.椅子展开后最大张角∠CBD=37°,且BD=BC,AB:BG:GC=1:2:3,座面EF与地面平行,当展开角最大时,请解答下列问题: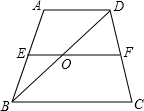 如图,在梯形ABCD中,AD∥BC,点E在AB上,点F在CD上,EF为中位线,EF与BD交于点O,若FO-EO=5,则BC-AD=
如图,在梯形ABCD中,AD∥BC,点E在AB上,点F在CD上,EF为中位线,EF与BD交于点O,若FO-EO=5,则BC-AD=