题目内容
 如图1是一张折叠椅子,图2是其侧面示意图,已知椅子折叠时长1.2米.椅子展开后最大张角∠CBD=37°,且BD=BC,AB:BG:GC=1:2:3,座面EF与地面平行,当展开角最大时,请解答下列问题:
如图1是一张折叠椅子,图2是其侧面示意图,已知椅子折叠时长1.2米.椅子展开后最大张角∠CBD=37°,且BD=BC,AB:BG:GC=1:2:3,座面EF与地面平行,当展开角最大时,请解答下列问题:(1)求∠CGF的度数;
(2)求座面EF与地面之间的距离.(可用计算器计算,结果保留两个有效数字,参考数据:sin71.5°≈0.948,cos71.5°≈0.317,tan71.5°≈2.989)
考点:解直角三角形的应用
专题:
分析:(1)根据等腰三角形的性质和三角形内角和定理可得∠BCD的度数,再根据平行线的性质可得∠CGF的度数;
(2)根据比的意义可得GC=1.2×
=0.6m,过点G作GK⊥DC于点K,在Rt△KCG中,根据三角函数可得座面EF与地面之间的距离.
(2)根据比的意义可得GC=1.2×
| 3 |
| 6 |
解答:解:(1)∵BD=BC,∠CBD=37°,
∴∠BDC=∠BCD=
=71.5°,
∵EF∥DC,
∴∠CGF=∠BCD=71.5°;
 (2)由题意知,AC=1.2m,
(2)由题意知,AC=1.2m,
∵AB:BG:GC=1:2:3,
GC=1.2×
=0.6m,
过点G作GK⊥DC于点K,
在Rt△KCG中,sin∠BCD=
,即sin75°=
,
∴GK=0.6sin75°≈0.57m.
答:座面EF与地面之间的距离约是0.57m.
∴∠BDC=∠BCD=
| 180°-37° |
| 2 |
∵EF∥DC,
∴∠CGF=∠BCD=71.5°;
 (2)由题意知,AC=1.2m,
(2)由题意知,AC=1.2m,∵AB:BG:GC=1:2:3,
GC=1.2×
| 3 |
| 6 |
过点G作GK⊥DC于点K,
在Rt△KCG中,sin∠BCD=
| GK |
| GC |
| GK |
| 0.6 |
∴GK=0.6sin75°≈0.57m.
答:座面EF与地面之间的距离约是0.57m.
点评:此题考查了等腰三角形的性质、三角形内角和定理、平行线的性质和三角函数的基本概念,主关键把实际问题转化为数学问题加以计算.

练习册系列答案
相关题目
已知a≠0,n是正整数,那么下列各式中错误的是( )
A、a-n=
| ||
B、a-n=(
| ||
| C、a-n=-an | ||
| D、a-n=(an)-1 |
 如图,在边长为6的正方形ABCD中,动点M从点A出发,沿A→B→C向终点C运动,连接DM交AC于点N,若点M运动所经过的路程为x(6≤x≤12),那么当△ADN为等腰三角形时,x的值为
如图,在边长为6的正方形ABCD中,动点M从点A出发,沿A→B→C向终点C运动,连接DM交AC于点N,若点M运动所经过的路程为x(6≤x≤12),那么当△ADN为等腰三角形时,x的值为 (1)如图,将A、B、C三个字母随机填写在三个空格中(每空填一个字母),求从左往右字母顺序恰好是A、B、C的概率;
(1)如图,将A、B、C三个字母随机填写在三个空格中(每空填一个字母),求从左往右字母顺序恰好是A、B、C的概率;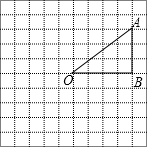 如图,方格纸中的每格都是边长为1的正方形,将△OAB(顶点都是正方形的顶点)绕点O按逆时针方向旋转90°得到△OA1B1.
如图,方格纸中的每格都是边长为1的正方形,将△OAB(顶点都是正方形的顶点)绕点O按逆时针方向旋转90°得到△OA1B1. 如图,在△ABC中,AC=BC,∠ACB=90°,点D是AB的中点,点E是AB边上一点.直线BF垂直于直线CE于点F,交CD于点G.
如图,在△ABC中,AC=BC,∠ACB=90°,点D是AB的中点,点E是AB边上一点.直线BF垂直于直线CE于点F,交CD于点G.