题目内容
某经销商代理销售一种手机,按协议,每卖出一部手机需另交品牌代理费100元,已知该种手机每部进价800元,销售单价为1200元时,每月能卖出100部,市场调查发现,若每部手机每让利50元,则每月可多售出40部.
(1)若每月要获取36000元利润,求让利价(利润=销售收入-进货成本-品牌代理费).
(2)设让利x元,月利润为y元,写出y与x的函数关系式,并求让利多少元时,月利润最大?
(1)若每月要获取36000元利润,求让利价(利润=销售收入-进货成本-品牌代理费).
(2)设让利x元,月利润为y元,写出y与x的函数关系式,并求让利多少元时,月利润最大?
考点:二次函数的应用,一元二次方程的应用
专题:
分析:(1)根据利润=销售收入-进货成本-品牌代理费=36000列方程,再解方程求出x的值即可;
(2)首先根据利润=销售收入-进货成本-品牌代理费=y,得到x和y的二次函数关系式,再依据函数的增减性求得最大利润.
(2)首先根据利润=销售收入-进货成本-品牌代理费=y,得到x和y的二次函数关系式,再依据函数的增减性求得最大利润.
解答:解:(1)设让利a元,依题意得,
(300-a)(0.8a+100)=36000,
解得,a1=100,a2=75,
经检验,a1,a2均符合题意.
答:让利100元或75元每月可获取利润36000元;
(2)依题意得:y=(300-x)(0.8x+100)=-
(x-87.5)2+36125,
∵-
<0
∴当x=87.5时,y有最大值,
答:让利87.5元,月利润最大.
(300-a)(0.8a+100)=36000,
解得,a1=100,a2=75,
经检验,a1,a2均符合题意.
答:让利100元或75元每月可获取利润36000元;
(2)依题意得:y=(300-x)(0.8x+100)=-
| 4 |
| 5 |
∵-
| 4 |
| 5 |
∴当x=87.5时,y有最大值,
答:让利87.5元,月利润最大.
点评:本题考查了二次函数的性质在实际生活中的应用.最大销售利润的问题常利函数的增减性来解答,我们首先要吃透题意,确定变量,建立函数模型,然后结合实际选择最优方案.其中要注意应该在自变量的取值范围内求最大值(或最小值),也就是说二次函数的最值不一定在x=-
时取得.
| b |
| 2a |

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 如图,D是△ABC的BC边的中点,AE平分∠BAC,AE⊥CE于点E,且AB=10,AC=16,则DE的长度为
如图,D是△ABC的BC边的中点,AE平分∠BAC,AE⊥CE于点E,且AB=10,AC=16,则DE的长度为 已知,如图,AC∥DE,AC=DE,BE=CF,求证:∠B=∠F.
已知,如图,AC∥DE,AC=DE,BE=CF,求证:∠B=∠F.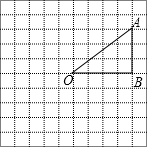 如图,方格纸中的每格都是边长为1的正方形,将△OAB(顶点都是正方形的顶点)绕点O按逆时针方向旋转90°得到△OA1B1.
如图,方格纸中的每格都是边长为1的正方形,将△OAB(顶点都是正方形的顶点)绕点O按逆时针方向旋转90°得到△OA1B1. 某小区改造项目中,要将一棵没有价值的树放倒,栽上白玉兰,在操作过程中,李师傅要直接把树放倒,张师傅不同意,他担心这样会损坏这棵树周围7米处的花园和雕塑.请你根据图中标注的测量数据:∠BCD=60°,∠DCA=5°,BD=6米,通过计算说明:张师傅的担心是否有必要?(供选数据:sin65°≈0.9,cos65°≈0.4,tan65°≈2.1,
某小区改造项目中,要将一棵没有价值的树放倒,栽上白玉兰,在操作过程中,李师傅要直接把树放倒,张师傅不同意,他担心这样会损坏这棵树周围7米处的花园和雕塑.请你根据图中标注的测量数据:∠BCD=60°,∠DCA=5°,BD=6米,通过计算说明:张师傅的担心是否有必要?(供选数据:sin65°≈0.9,cos65°≈0.4,tan65°≈2.1, 用大小相同的立方体搭一个几何体,它的主视图和俯视图如图,则搭这个几何体需要
用大小相同的立方体搭一个几何体,它的主视图和俯视图如图,则搭这个几何体需要