题目内容
4. 如图,△ABC中,D、E、F为BC、AD、BE的中点,若△CEF的面积是3,则△ABC的面积是12.
如图,△ABC中,D、E、F为BC、AD、BE的中点,若△CEF的面积是3,则△ABC的面积是12.
分析 根据三角形的面积公式得到:三角形的中线将三角形分为面积相等的两部分,据此进行答题即可.
解答 解:∵点F是BE的中点,
∴S△EFC=$\frac{1}{2}$S△BCE.
又∵点D是BC的中点,
∴S△BDE=$\frac{1}{2}$S△BCE,S△ABD=$\frac{1}{2}$S△ABC,
∴S△BDE=S△EFC=3,S△ABC=2S△ABD.
又∵点E是AD的中点,
∴S△BDE=$\frac{1}{2}$S△ABD,即S△ABD=2S△BDE=6,
∴S△ABC=2S△ABD=12.
故答案是:12.
点评 本题考查了三角形面积:三角形面积等于底边与底边上的高乘积的一半;等底等高的两三角形面积相等,等高的两三角形面积的比等于底边的比.

练习册系列答案
相关题目
12.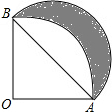 如图,扇形AOB的半径为1,∠AOB=90°,以AB为直径画半圆,则图中的阴影部分的面积为( )
如图,扇形AOB的半径为1,∠AOB=90°,以AB为直径画半圆,则图中的阴影部分的面积为( )
 如图,扇形AOB的半径为1,∠AOB=90°,以AB为直径画半圆,则图中的阴影部分的面积为( )
如图,扇形AOB的半径为1,∠AOB=90°,以AB为直径画半圆,则图中的阴影部分的面积为( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$π | C. | $\frac{1}{8}$π | D. | π |
19.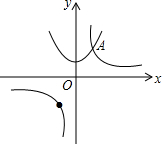 如图,抛物线y=x2+1与双曲线y=$\frac{k}{x}$的交点A的横坐标是1,则关于x的不等式$\frac{k}{x}<{x^2}$+1的解集是( )
如图,抛物线y=x2+1与双曲线y=$\frac{k}{x}$的交点A的横坐标是1,则关于x的不等式$\frac{k}{x}<{x^2}$+1的解集是( )
 如图,抛物线y=x2+1与双曲线y=$\frac{k}{x}$的交点A的横坐标是1,则关于x的不等式$\frac{k}{x}<{x^2}$+1的解集是( )
如图,抛物线y=x2+1与双曲线y=$\frac{k}{x}$的交点A的横坐标是1,则关于x的不等式$\frac{k}{x}<{x^2}$+1的解集是( )| A. | x>1 | B. | x<0 | C. | 0<x<1 | D. | x<0或x>1 |
 在直角梯形ABCD中,AB∥CD,∠BCD=RT∠,AB=AD=10cm,BC=8cm,点P从点A出发,以每秒3cm的速度沿直线ABCD方向运动,点Q从点D出发以每秒2cm的速度沿线段DC方向向点C运动,已知动点P,Q同时出发,当点Q运动到点C时,P,Q运动停止,设运动时间为t.
在直角梯形ABCD中,AB∥CD,∠BCD=RT∠,AB=AD=10cm,BC=8cm,点P从点A出发,以每秒3cm的速度沿直线ABCD方向运动,点Q从点D出发以每秒2cm的速度沿线段DC方向向点C运动,已知动点P,Q同时出发,当点Q运动到点C时,P,Q运动停止,设运动时间为t.