题目内容
2.把抛物线y=$\frac{1}{2}$(x-4)2先向左平移3个单位,再向下平移4个单位,所得到的抛物线是( )| A. | y=$\frac{1}{2}$(x-4)2-4 | B. | y=$\frac{1}{2}$x2 | C. | y=$\frac{1}{2}$(x-7)2-4 | D. | y=$\frac{1}{2}$(x-1)2-4 |
分析 抛物线的平移,实际上就是顶点的平移,先求出原抛物线的顶点坐标,再根据平移规律,推出新抛物线的顶点坐标,根据顶点式可求新抛物线的解析式.
解答 解:原抛物线的顶点为(4,0),向左平移3个单位,再向下平移4个单位,那么新抛物线的顶点为(1,-4);
可设新抛物线的解析式为y=$\frac{1}{2}$(x-h)2+k代入得:y=$\frac{1}{2}$(x-1)2-4.
故选:D.
点评 考查了二次函数图象与几何变换,抛物线平移不改变二次项的系数的值,解决本题的关键是得到新抛物线的顶点坐标.

练习册系列答案
相关题目
12.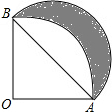 如图,扇形AOB的半径为1,∠AOB=90°,以AB为直径画半圆,则图中的阴影部分的面积为( )
如图,扇形AOB的半径为1,∠AOB=90°,以AB为直径画半圆,则图中的阴影部分的面积为( )
 如图,扇形AOB的半径为1,∠AOB=90°,以AB为直径画半圆,则图中的阴影部分的面积为( )
如图,扇形AOB的半径为1,∠AOB=90°,以AB为直径画半圆,则图中的阴影部分的面积为( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$π | C. | $\frac{1}{8}$π | D. | π |
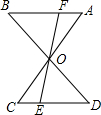 如图所示,已知△AOB≌△COD,△COE≌△AOF,求证:△BOF≌△DOE.
如图所示,已知△AOB≌△COD,△COE≌△AOF,求证:△BOF≌△DOE.