题目内容
3.现有两个完全一样的正方形纸片,面积都是3,把它们拼成一个边长为a的正方形.思考下面的命题:①a可以用数轴上的点表示;
②a是x-3<0的一个解;
③a是一个无限不循环小数;
④a是6的算术平方根;
⑤新拼成的正方形对角线长为2$\sqrt{3}$.
其中真命题的个数是( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 利用正方形的面积得出边长对各个小题进行判断后即可确定答案.
解答 解:因为两个完全一样的正方形纸片,面积都是3,把它们拼成一个边长为a的正方形,
可得:a=$\sqrt{6}$,
所以可得:①a可以用数轴上的点表示,正确;
②a是x-3<0的一个解,正确;
③a是一个无限不循环小数,正确;
④a是6的算术平方根,正确;
⑤新拼成的正方形对角线长为2$\sqrt{3}$,正确.
故选D.
点评 本题考查了命题与定理的知识,解题的关键是利用正方形的面积得出边长.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.对于△ABC,下列叙述错误的是( )
| A. | 如果∠A=∠B=∠C,那么△ABC一定是锐角三角形 | |
| B. | 如果∠A=∠B+∠C,那么△ABC一定是直角三角形 | |
| C. | 如果∠A:∠B:∠C=1:3:5,那么△ABC是钝角三角形 | |
| D. | 如果∠A=40°,∠B=3∠C,那么△ABC是锐角三角形 |
12.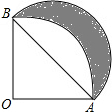 如图,扇形AOB的半径为1,∠AOB=90°,以AB为直径画半圆,则图中的阴影部分的面积为( )
如图,扇形AOB的半径为1,∠AOB=90°,以AB为直径画半圆,则图中的阴影部分的面积为( )
 如图,扇形AOB的半径为1,∠AOB=90°,以AB为直径画半圆,则图中的阴影部分的面积为( )
如图,扇形AOB的半径为1,∠AOB=90°,以AB为直径画半圆,则图中的阴影部分的面积为( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$π | C. | $\frac{1}{8}$π | D. | π |
 在直角梯形ABCD中,AB∥CD,∠BCD=RT∠,AB=AD=10cm,BC=8cm,点P从点A出发,以每秒3cm的速度沿直线ABCD方向运动,点Q从点D出发以每秒2cm的速度沿线段DC方向向点C运动,已知动点P,Q同时出发,当点Q运动到点C时,P,Q运动停止,设运动时间为t.
在直角梯形ABCD中,AB∥CD,∠BCD=RT∠,AB=AD=10cm,BC=8cm,点P从点A出发,以每秒3cm的速度沿直线ABCD方向运动,点Q从点D出发以每秒2cm的速度沿线段DC方向向点C运动,已知动点P,Q同时出发,当点Q运动到点C时,P,Q运动停止,设运动时间为t.