题目内容
19.解方程(1)$\frac{2x}{x-1}-\frac{4x-1}{{{x^2}-x}}$=2
(2)(x-2)(x+3)=5.
分析 (1)分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解;
(2)方程整理后,利用公式法求出解即可.
解答 解:(1)去分母得:2x2-4x+1=2x2-2x,
解得:x=$\frac{1}{2}$,
经检验x=$\frac{1}{2}$是分式方程的解;
(2)方程整理得:x2+x-11=0,
这里a=1,b=1,c=-11,
∵△=1+44=45,
∴x=$\frac{-1±3\sqrt{5}}{2}$.
点评 此题考查了解分式方程,以及解一元二次方程-公式法,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
9.若不等式(a+1)x>a+1的解集是x<1,则a必满足( )
| A. | a<-1 | B. | a>-1 | C. | a<0 | D. | a<1 |
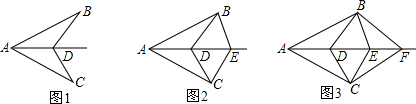
14.已知AB=AC,AD为∠BAC的角平分线,D、E、F…为∠BAC的角平分线上的若干点.如图1,连接BD、CD,图中有1对全等三角形;如图2,连接BD、CD、BE、CE,图中有3对全等三角形;如图3,连接BD、CD、CE、BF、CF,图中有6对全等三角形;依此规律,第8个图形中有全等三角形( )

| A. | 24对 | B. | 28对 | C. | 36对 | D. | 72对 |
11.已知式子$\frac{{x}^{2}-4}{2x-4}$的值为零,则x的值为( )
| A. | 2 | B. | -2 | C. | ±2 | D. | 0 |
8.直角三角形的两条直角边的长分别为5,12,则斜边上的高线的长为( )
| A. | $\frac{80}{13}$cm | B. | 13cm | C. | $\frac{13}{2}$cm | D. | $\frac{60}{13}$cm |
 解不等式组$\left\{\begin{array}{l}{1+2x>3+x}\\{5x≥4x-1}\end{array}\right.$,并把它的解集在如下的数轴上表示出来.
解不等式组$\left\{\begin{array}{l}{1+2x>3+x}\\{5x≥4x-1}\end{array}\right.$,并把它的解集在如下的数轴上表示出来. 如图所示,E为AB延长线上的一点,AC⊥BC,AD⊥BD,AC=AD
如图所示,E为AB延长线上的一点,AC⊥BC,AD⊥BD,AC=AD