��Ŀ����
2��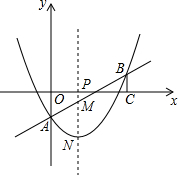 ��ͼ��ʾ��������y=$\frac{1}{4}$x2+mx+n��ֱ��y=$\frac{1}{2}$x-2�ཻ�ڵ�A�͵�B�����е�A��y���ϣ�����B��BC��x�ˣ�����Ϊ��C��6��0����
��ͼ��ʾ��������y=$\frac{1}{4}$x2+mx+n��ֱ��y=$\frac{1}{2}$x-2�ཻ�ڵ�A�͵�B�����е�A��y���ϣ�����B��BC��x�ˣ�����Ϊ��C��6��0������1���������ߵĽ���ʽ��
��2����P���߶�OC��һ�㣮����P��PM��x�ύֱ��AB�ڵ�M�����������ڵ�N�������P������Ϊ��t��0�����߶�MN�ij�Ϊs����s��t�ĺ�����ϵʽ��
��3������MB��NC���Ƿ���ڵ�Pʹ�ı���MNCBΪƽ���ı��Σ������ڣ������P�����ꣻ�������ڣ���˵�����ɣ�
���� ��1�������A��B�����꣬���ô���ϵ��������κ����Ľ���ʽ��
��2�����ݽ���ʽ�ֱ��ʾM��N��������꣬��MN=PM+PN��PN-PM���м��㣻
��3�����ڣ�����MN=BC�з��̿ɵý��ۣ�
��� 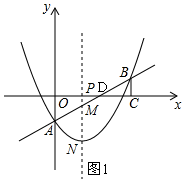 �⣺��1����x=6ʱ��y=$\frac{1}{2}$��6-2=1��
�⣺��1����x=6ʱ��y=$\frac{1}{2}$��6-2=1��
��B��6��1����
��x=0ʱ��y=-2��$\left\{\begin{array}{l}{\frac{1}{4}{x}^{2}+6m+n=1}\\{n=-2}\end{array}\right.$
��A��0��-2����
��A��0��-2����B��6��1�����������ߵĽ���ʽ�еã�$\left\{\begin{array}{l}{\frac{1}{4}��{6}^{2}+6m+n=1}\\{n=-2}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{m=-1}\\{n=-2}\end{array}\right.$��
�������ߵĽ���ʽΪ��y=$\frac{1}{4}$x2-x-2��
��2��������ã�M��t��$\frac{1}{2}$t-2����N��t��$\frac{1}{4}{t}^{2}$-t-2����
��y=0ʱ��$\frac{1}{2}$x-2=0��
x=4��
��D��4��0����
��0��t��4ʱ����ͼ1��PM=2-$\frac{1}{2}$t��PN=-$\frac{1}{4}{t}^{2}$+t+2��
��MN=PN-PM=-$\frac{1}{4}{t}^{2}$+t+2-2+$\frac{1}{2}$t=-$\frac{1}{4}{t}^{2}$+$\frac{3}{2}$t��
��s=-$\frac{1}{4}{t}^{2}$+$\frac{3}{2}$t��
��4��t��6ʱ����ͼ2��PM=$\frac{1}{2}$t-2��PN=-$\frac{1}{4}{t}^{2}$+t+2��
��MN=PM+PN=$\frac{1}{2}$t-2-$\frac{1}{4}{t}^{2}$+t+2=-$\frac{1}{4}{t}^{2}$+$\frac{3}{2}$t��
��s=-$\frac{1}{4}{t}^{2}$+$\frac{3}{2}$t��
����������s��t�ĺ�����ϵʽΪ��s=-$\frac{1}{4}{t}^{2}$+$\frac{3}{2}$t��
��3�����ڣ���ͼ3��
��PM��x�ᣬBC��x�ˣ�
��PM��BC��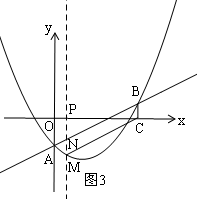
��MN��BC��
�൱MN=BCʱ���ı���MNCBΪƽ���ı��Σ�
��-$\frac{1}{4}{t}^{2}$+$\frac{3}{2}$t=1��
��ã�t=3$��\sqrt{5}$��
��P��3+$\sqrt{5}$��0����3-$\sqrt{5}$��0����
���� �����Ƕ��κ������ۺ��⣬�Ѷ����У����������ô���ϵ��������κ����Ľ���ʽ��������������Ľ��㡢ƽ���ı��ε��ж����ں������ۺ����г����ú����Ľ���ʽ��ʾ�߶εij�������Ҳ����ˣ���Ҫע��������ͼ���ص㣮

 ��������������������ϵ�д�
��������������������ϵ�д�| A�� | x-5 | B�� | 5-x | C�� | 5+x | D�� | -5-x |
| A�� | һ����������н�����l%����ô��100�ν���Ȼ����һ�ν� | |
| B�� | һ���˿����У������ȡһ���Ǻ���K�����DZ�Ȼ�¼� | |
| C�� | һ�������Ĵ���װ��3������5��������������һ�����Ǻ���ĸ�����$\frac{3}{5}$ | |
| D�� | ��Ȼ�¼��ĸ���Ϊ1 |
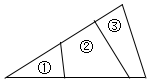 ijͬѧ��С�İ�һ�������β�����������飬��Ҫȥ����������һ����ȫһ���ģ���ʡ�ĵİ취�Ǵ��� ��������
ijͬѧ��С�İ�һ�������β�����������飬��Ҫȥ����������һ����ȫһ���ģ���ʡ�ĵİ취�Ǵ��� ��������| A�� | �� | B�� | �� | C�� | �� | D�� | �٢ڢ� |

��1�����������еĹ�����գ�
| a-1 | a |
| a+6 | a+7 |
��3��ij��С������������������μ���ë���������ùھ�����������֮����51��
��С����24�Ŷ�ڵģ�
�ڱ���1�������ģ�
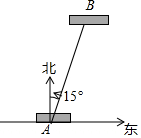 ��ͼ��һ�Ҵ���A�����պ������50 ����λ��B���ľ������������÷���;����������մ�����ھ�������λ����ƫ��15�㣬50���
��ͼ��һ�Ҵ���A�����պ������50 ����λ��B���ľ������������÷���;����������մ�����ھ�������λ����ƫ��15�㣬50���