题目内容
1.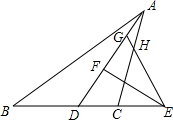 如图,在△ABC中,2AB=3AC,AD为△BAC的角平分线,点H在线段AC上,且CH=2AH,E为BC延长线上的一点,连接EH并延长交AD于点G,使EG=ED,过点E作EF⊥AD于点F,则AG:FG=4:7.
如图,在△ABC中,2AB=3AC,AD为△BAC的角平分线,点H在线段AC上,且CH=2AH,E为BC延长线上的一点,连接EH并延长交AD于点G,使EG=ED,过点E作EF⊥AD于点F,则AG:FG=4:7.
分析 由2AB=3AC,CH=2AH,得到AC=3AH,AB=$\frac{3}{2}$AC=$\frac{3}{2}$×3AH=$\frac{9}{2}$AH,于是得到$\frac{AB}{AH}=\frac{9}{2}$,由于AD为△BAC的角平分线,得到∠BAD=∠HAG,根据等腰三角形的性质三线合一得到∠GDE=∠DGE,DG=2DF=2FG,求得△ABD∽△AHG,列比例式代入数据即可得到结果.
解答 解:∵2AB=3AC,CH=2AH,
∴AC=3AH,AB=$\frac{3}{2}$AC=$\frac{3}{2}$×3AH=$\frac{9}{2}$AH,
∴$\frac{AB}{AH}=\frac{9}{2}$,
∵AD为△BAC的角平分线,
∴∠BAD=∠HAG,
∵EF⊥AD,EG=DE,
∴∠GDE=∠DGE,DG=2DF=2FG,
∴∠ADB=∠AGH,
∴△ABD∽△AHG,
∴$\frac{AD}{AG}=\frac{AB}{AH}=\frac{9}{2}$,
∴AG=$\frac{2}{9}$AD,
∴DG=$\frac{7}{9}$AD,FG=$\frac{1}{2}$DG=$\frac{7}{18}$AD,
∴$\frac{AG}{FG}=\frac{\frac{2}{9}AD}{\frac{7}{18}AD}$=$\frac{4}{7}$.
故答案为:$\frac{4}{7}$.
点评 本题考查了相似三角形的判定和性质,等腰三角形的性质,推出△ABD∽△AHG是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.直线y=2x+3与坐标轴围成的面积是( )
| A. | $\frac{3}{4}$ | B. | 3 | C. | $\frac{9}{4}$ | D. | 6 |
13.“垃圾分一分,环境美十分”.如果要了解人们进行垃圾分类的情况,则最合适的调查方式是( )
| A. | 普查 | B. | 抽样调查 | ||
| C. | 在社会上随机调查 | D. | 在学校里随机调查 |
10. 如图,△ABC是⊙O的内接三角形,∠OAB=35°,则∠ACB的度数为( )
如图,△ABC是⊙O的内接三角形,∠OAB=35°,则∠ACB的度数为( )
 如图,△ABC是⊙O的内接三角形,∠OAB=35°,则∠ACB的度数为( )
如图,△ABC是⊙O的内接三角形,∠OAB=35°,则∠ACB的度数为( )| A. | 35° | B. | 55° | C. | 60° | D. | 70° |
 如图,已知AB∥CD,EF平分∠AEG,∠EFG=50°,则∠EGF的度数是80°.
如图,已知AB∥CD,EF平分∠AEG,∠EFG=50°,则∠EGF的度数是80°. 阅读材料:
阅读材料: 如图,在10×10正方形网格中,每个小正方形的边长均为1个单位.
如图,在10×10正方形网格中,每个小正方形的边长均为1个单位.