题目内容
 如图,AO⊥BC于点O,且∠DOC=5∠AOD-12°,求∠BOD的度数.
如图,AO⊥BC于点O,且∠DOC=5∠AOD-12°,求∠BOD的度数.考点:垂线
专题:
分析:根据垂线的定义,可得∠AOB与∠AOC的度数,根据余角的定义,可得∠AOD与∠COD的关系,根据代入消元,可得∠AOD的度数,根据角的和差,可得答案.
解答:解:由AO⊥BC于点O,得
∠AOB=∠AOC=90°.
由余角的定义,得
∠AOD+∠COD=90°①.
把∠DOC=5∠AOD-12°代入①,得
∠AOD+5∠AOD-12°=90°,
解得∠AOD=17°,
由角的和差,得
∠BOD=∠AOB+∠AOD=90°+17°=107°.
∠AOB=∠AOC=90°.
由余角的定义,得
∠AOD+∠COD=90°①.
把∠DOC=5∠AOD-12°代入①,得
∠AOD+5∠AOD-12°=90°,
解得∠AOD=17°,
由角的和差,得
∠BOD=∠AOB+∠AOD=90°+17°=107°.
点评:本题考查了垂线,利用了垂线的定义,余角的定义,代入消元法得出∠AOD的度数是解题关键.

练习册系列答案
相关题目
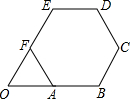 如图,正六边形ABCDEF的边长为2
如图,正六边形ABCDEF的边长为2 已知,如图,MN是⊙O的弦,AB是⊙O的直径,AB⊥MN,垂足为点P,半径OC,OD分别交MN于点E,F,且OE=OF.求证:
已知,如图,MN是⊙O的弦,AB是⊙O的直径,AB⊥MN,垂足为点P,半径OC,OD分别交MN于点E,F,且OE=OF.求证:

 如图,直线AB,CD相交于点E,FE⊥AB,若∠FEC-∠AEC=20°,那么∠AED的度数是
如图,直线AB,CD相交于点E,FE⊥AB,若∠FEC-∠AEC=20°,那么∠AED的度数是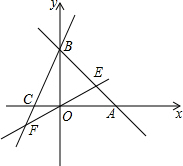 直线AB:y=-x+b分别与x,y轴交于A(6,0)、B两点,过点B的直线交x轴负半轴于C,且OB:OC=3:1.
直线AB:y=-x+b分别与x,y轴交于A(6,0)、B两点,过点B的直线交x轴负半轴于C,且OB:OC=3:1.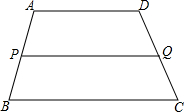 如图,在梯形ABCD中,AD∥BC,P是AB的中点,过P点作AD的平行线交DC于Q点.
如图,在梯形ABCD中,AD∥BC,P是AB的中点,过P点作AD的平行线交DC于Q点.