题目内容
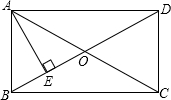 在矩形ABCD中,AD=8cm,对角线比AB边长4cm,则AB=
在矩形ABCD中,AD=8cm,对角线比AB边长4cm,则AB=考点:矩形的性质
专题:
分析:根据矩形的性质得出∠BAD=90°,AC=BD,设AB=acm,则AC=BD=(a+4)cm,在Rt△BAD中,由勾股定理得出方程82+a2=(a+4)2,求出a,根据三角形的面积求出AE即可.
解答:解:∵四边形ABCD是矩形,
∴∠BAD=90°,AC=BD,
设AB=acm,则AC=BD=(a+4)cm,
在Rt△BAD中,由勾股定理得:82+a2=(a+4)2,
解得;a=6cm,
即AB=6cm,BD=10cm,
根据三角形面积公式得;
AB×AD=
BD×AE,
6×8=10×AE,
∴AE=4.8cm.
故答案为:6cm,4.8cm.
∴∠BAD=90°,AC=BD,
设AB=acm,则AC=BD=(a+4)cm,
在Rt△BAD中,由勾股定理得:82+a2=(a+4)2,
解得;a=6cm,
即AB=6cm,BD=10cm,
根据三角形面积公式得;
| 1 |
| 2 |
| 1 |
| 2 |
6×8=10×AE,
∴AE=4.8cm.
故答案为:6cm,4.8cm.
点评:本题考查了矩形的性质,勾股定理,三角形的面积的应用,解此题的关键是求出AB的长,注意:矩形的每个角都是直角,矩形的对角线相等,难度适中.

练习册系列答案
相关题目
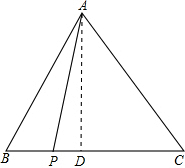 如图,在△ABC中,AB=AC=1,BC边上有2011个不同的点P1,P2,…,P2011,记mi=APi2+BPi•PiC(i=1,2,…,2011),则m1+m2+…+m2011=
如图,在△ABC中,AB=AC=1,BC边上有2011个不同的点P1,P2,…,P2011,记mi=APi2+BPi•PiC(i=1,2,…,2011),则m1+m2+…+m2011=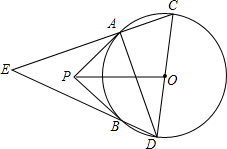 如图,PA,PB是⊙O的两条切线,切线分别是A,B.CD是⊙O的直径,直线AC,BD相交于点E.
如图,PA,PB是⊙O的两条切线,切线分别是A,B.CD是⊙O的直径,直线AC,BD相交于点E.
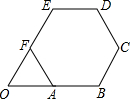 如图,正六边形ABCDEF的边长为2
如图,正六边形ABCDEF的边长为2 已知,如图,MN是⊙O的弦,AB是⊙O的直径,AB⊥MN,垂足为点P,半径OC,OD分别交MN于点E,F,且OE=OF.求证:
已知,如图,MN是⊙O的弦,AB是⊙O的直径,AB⊥MN,垂足为点P,半径OC,OD分别交MN于点E,F,且OE=OF.求证:
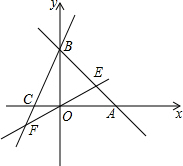 直线AB:y=-x+b分别与x,y轴交于A(6,0)、B两点,过点B的直线交x轴负半轴于C,且OB:OC=3:1.
直线AB:y=-x+b分别与x,y轴交于A(6,0)、B两点,过点B的直线交x轴负半轴于C,且OB:OC=3:1.