题目内容
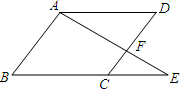在?ABCD中，延长BC到E，使CE：BC=1：2，连接AE交DC于F，求：S△AFD：S△EFC=考点：相似三角形的判定与性质,平行四边形的性质
专题：
分析：如图，证明△ADF∽△ECF，得到
=(
)2；求出
的值，即可解决问题．
| S△ADF |
| S△EFC |
| AD |
| CE |
| AD |
| CE |
解答：解：如图，∵四边形ABCD为平行四边形，
∴AD=BC，AD∥CE；
∴△ADF∽△ECF，
∴
=(
)2；
∵CE：BC=1：2，
∴AD：CE=2：1，
∴
=(
)2=
，
故答案为4：1．
解：如图，∵四边形ABCD为平行四边形，∴AD=BC，AD∥CE；
∴△ADF∽△ECF，
∴
| S△ADF |
| S△EFC |
| AD |
| CE |
∵CE：BC=1：2，
∴AD：CE=2：1，
∴
| S△ADF |
| S△EFC |
| AD |
| CE |
| 4 |
| 1 |
故答案为4：1．
点评：该题主要考查了平行四边形的性质、相似三角形的判定及其性质等几何知识点及其应用问题；应牢固掌握平行四边形的性质、相似三角形的判定及其性质等几何知识点．
练习册系列答案
相关题目
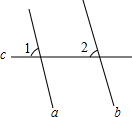如图，a∥b，a、b被c所截，得到∠1=∠2的依据是（ ）| A、两直线平行，同位角相等 |
| B、两直线平行，内错角相等 |
| C、同位角相等，两直线平行 |
| D、内错角相等，两直线平行 |
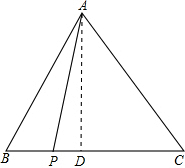如图，在△ABC中，AB=AC=1，BC边上有2011个不同的点P1，P2，…，P2011，记mi=APi2+BPi•PiC（i=1，2，…，2011），则m1+m2+…+m2011=
如图，正六边形ABCDEF的边长为2
已知，如图，MN是⊙O的弦，AB是⊙O的直径，AB⊥MN，垂足为点P，半径OC，OD分别交MN于点E，F，且OE=OF．求证：
