题目内容
13．
如图，已知△ABC的三个顶点均在正方形网格的格点上，则cosA的值为$\frac{2\sqrt{5}}{5}$．
分析 直接利用网格构建直角三角形，再利用勾股定理得出AD，AB的长，进而利用余弦值的定义得出答案．
解答 
解：如图所示：连接BD，
可得：∠CDB=90°，BD=$\sqrt{2}$，AD=2$\sqrt{2}$，AB=$\sqrt{10}$，
故cosA=$\frac{AD}{AB}$=$\frac{2\sqrt{2}}{\sqrt{10}}$=$\frac{2\sqrt{5}}{5}$．
故答案为：$\frac{{2\sqrt{5}}}{5}$．
点评 此题主要考查了锐角三角函数的定义以及勾股定理，正确掌握锐角三角函数关系是解题关键．
练习册系列答案
相关题目
4．下列运算中，正确的是（ ）
| A． | a2•a6=a12 | B． | （a3）3=a6 | C． | （-2a）3=6a3 | D． | （a2）3=a6 |
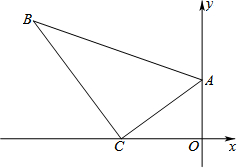如图，一块直角三角板ABC放置在平面直角坐标系中，∠B=30°，顶点A的坐标为（0，6），直角顶点C的坐标为（-8，0）．
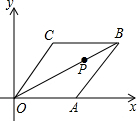如图，在平面直角坐标系xOy中，菱形OABC的顶点A在x轴上，顶点B的坐标为（8，4）点P的对角线OB上一个动点，点D的坐标为（0，-2），当DP与AP之和最小时，点P的坐标为（$\frac{4}{3}$，$\frac{2}{3}$）．