题目内容
14．当x=-$\frac{5}{3}$时，求（1-x）2-4（1-x2）+4（1+x）2的值．分析 将原式利用完全平方公式因式分解后，把x的值代入计算可得．
解答 解：原式=（1-x）2-4（1-x）（1+x）+4（1+x）2
=[1-x-2（1+x）]2
=（1-x-2-2x）2
=（-1-3x）2
=（1+3x）2，
当x=-$\frac{5}{3}$时，
原式=（1-3×$\frac{5}{3}$）2
=（-4）2
=16．
点评 本题主要考查整式的化简求值，观察到原式符合完全平方公式并且利用公式因式分解进行简便计算是关键．
练习册系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
如图，在△ABC中
5．下列等式成立的是（ ）
| A． | $\sqrt{4}$=±2 | B． | $\frac{22}{7}$=π | C． | $\sqrt{8}={2^{\frac{3}{2}}}$ | D． | |a+b|=a+b |
2．九年级一班数学老师对全班学生在模拟考试中A卷成绩进行统计后，制成如下的统计表：
则该班学生A卷成绩的众数和中位数分别是（ ）
| 成绩（分） | 80 | 82 | 84 | 86 | 87 | 90 |
| 人数 | 8 | 12 | 9 | 3 | 5 | 8 |
| A． | 82分，82分 | B． | 82分，83分 | C． | 80分，82分 | D． | 82分，84分 |
19．当前，雾霾严重．治理雾霾方法之一是将已生产的PM2.5吸纳降解．研究表明：雾霾的程度随城市中心区立体绿化面积的增大而减小，在这个问题中，自变量是（ ）
| A． | 城市中心立体绿化面积 | B． | PM2.5 | ||
| C． | 雾霾 | D． | 雾霾程度 |
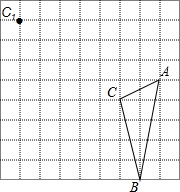在边长为1的正方形网格中有△ABC，将这个三角形进行平移，使C点的对称点C1，