Question

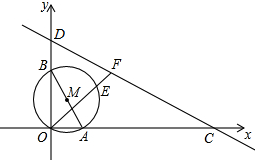如图，⊙M过坐标原点O，分别交两坐标轴于A（1，O），B（0，2）两点，直线CD交x轴于点C（6，0），交y轴于点D（0，3），过点O作直线OF，分别交⊙M于点E，交直线CD于点F．
（1）∠CDO=∠BAO；
（2）求证：OE•OF=OA•OC；
（3）若OE=

3

2

2

，试求点F的坐标．

Answer 1

考点：圆的综合题

专题：代数几何综合题

分析：（1）利用tan∠CDO=cot∠BAO求出∠CDO=∠BAO，
（2）连接AE，圆周角相等得出△OCF∽△OEA．再利用比例式求证．
（3）先求出OF的长度，再利用方程组求出交点，得出点P的坐标．

解答：
证明：（1）如图：
∵C（6，0），D（0，3），
∴tan∠CDO=

OC

OD

=

6

3

=2，
∵A（1，O），B（0，2），
tan∠BAO=

OB

OA

=2，
∴∠CDO=∠BAO，
（2）如图，连接AE，

由（1）知∠CDO=∠BAO，
∴∠OCD=∠OBA，
∵∠OBA=∠OEA，
∴∠OCD=∠OEA，
∴△OCF∽△OEA，
∴

OE

OC

=

OA

OF

∴OE•OF=OA•OC；
（3）由（2）得OE•OF=OA•OC，
∵OA=1，0C=6，OE=

3 2

2

，
∴OF═

OA•OC

OE

=

1×6

3 2 2

=2

2

设F（x，y）
∴x²+y²=8，
∵直线CD的函数式为：y=-

1

2

x+3
∴组成的方程组为

x2+y2=8 y=- 1 2 x+3

，
解得

x=2 y=2

或

x= 2 5 y= 14 5

∴F的坐标为：（2，2）或（

2

5

，

14

5

）．

点评：本题主要考查了圆的综合题，解题的关键是利用圆周角相等得出△OCF∽△OEA．