题目内容
在平面直角坐标系中有两点A(1,-3),B(5,-4),试在x轴上找到两点D(a,0),C(a+2,0),若四形ABCD周长最短,则a的值为 .
考点:轴对称-最短路线问题,坐标与图形性质
专题:
分析:首先作出A点对称点A1,进而连接A1B交于点D,作出C点,则四边形ABCD的周长最短.
解答:
解:如图所示,∵A1是A点的对称点,
∴FA1=3,
作BE⊥AA1 交延长线于E,
则EA1=7,
∵FC∥EB,EB=4,
∴
=
,
即;
=
,
∴FD=
,
∴a=
-1=
.
故答案为:
.

解:如图所示,∵A1是A点的对称点,
∴FA1=3,
作BE⊥AA1 交延长线于E,
则EA1=7,
∵FC∥EB,EB=4,
∴
| FD |
| EB |
| FA1 |
| A1E |
即;
| FD |
| 4 |
| 3 |
| 7 |
∴FD=
| 12 |
| 7 |
∴a=
| 12 |
| 7 |
| 5 |
| 7 |
故答案为:
| 5 |
| 7 |
点评:此题主要考查了轴对称求最短路径,根据在一条直线上找一点使它到直线同旁的两个点的距离之和最小是解题关键.

练习册系列答案
相关题目
把多项式(m+1)(m-1)+(m+1)提取公因式m+1后,余下的部分是( )
| A、m+1 | B、m-1 |
| C、m | D、2 m+1 |
平面直角坐标系中有A(-2,-1),B(-4,3),C(0,0),则三角形ABC的面积为( )
| A、5 | B、6 | C、8 | D、3 |
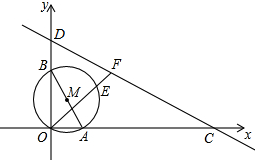 如图,⊙M过坐标原点O,分别交两坐标轴于A(1,O),B(0,2)两点,直线CD交x轴于点C(6,0),交y轴于点D(0,3),过点O作直线OF,分别交⊙M于点E,交直线CD于点F.
如图,⊙M过坐标原点O,分别交两坐标轴于A(1,O),B(0,2)两点,直线CD交x轴于点C(6,0),交y轴于点D(0,3),过点O作直线OF,分别交⊙M于点E,交直线CD于点F. 如图,OB是⊙O的半径,弦AB=OB,直径CD⊥AB.若点P是线段OD上的动点,连接PA,则∠PAB的度数可以是
如图,OB是⊙O的半径,弦AB=OB,直径CD⊥AB.若点P是线段OD上的动点,连接PA,则∠PAB的度数可以是 某校开展“好书伴我成长”的读书活动,为了解八年级450名学生的读书情况,随机调查了八年级50名学生本学期读书的册数,并将统计数据制成了扇形统计图,则该校八年级读书册数等于3册的约有
某校开展“好书伴我成长”的读书活动,为了解八年级450名学生的读书情况,随机调查了八年级50名学生本学期读书的册数,并将统计数据制成了扇形统计图,则该校八年级读书册数等于3册的约有 如图,直线a、b相交于点O,∠1=50°,则∠2=
如图,直线a、b相交于点O,∠1=50°,则∠2= 如图,已知∠1=∠2,∠3=73°,则∠4的度数为
如图,已知∠1=∠2,∠3=73°,则∠4的度数为