题目内容
1.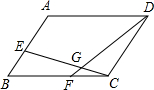 如图,若平行四边形ABCD的面积是1,E在AB上,F在BC上,且AE:EB=5:3,BF:FC=3:2,EC和FD相交于G,则△GFC的面积为$\frac{3}{115}$.
如图,若平行四边形ABCD的面积是1,E在AB上,F在BC上,且AE:EB=5:3,BF:FC=3:2,EC和FD相交于G,则△GFC的面积为$\frac{3}{115}$.
分析 首先过点F作FH∥AB,交EC于点H,可得△FCH∽△BCE,根据相似三角形的面积比等于相似比的平方,可得$\frac{{S}_{△FCH}}{{S}_{△BCE}}$=($\frac{FC}{BC}$)2,然后由同高三角形的面积比等于底的比,即可求得△FCH的面积,再由相似三角形的对应边的比,即可求得CG:HG的值,继而求得答案.
解答 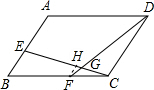 解:如图,过点F作FH∥AB,交EC于点H,
解:如图,过点F作FH∥AB,交EC于点H,
∴△FCH∽△BCE,
∴$\frac{{S}_{△FCH}}{{S}_{△BCE}}$=($\frac{FC}{BC}$)2,
∵平行四边形ABCD的面积是1,AE:EB=5:3,
∴S△BCE=$\frac{3}{5+3}$×$\frac{1}{2}$×1=$\frac{3}{16}$,
∵BF:FC=3:2,
∴FH:BE=CF:BF=2:5,
∴S△CFH=$\frac{4}{25}$×$\frac{3}{16}$=$\frac{3}{100}$,
∵BE:CD=3:8,
∴FH:CD=3:20,
∴HG:CG=3:20,
∴S△CFH=$\frac{20}{23}$×$\frac{3}{100}$=$\frac{3}{115}$.
故答案为:$\frac{3}{115}$.
点评 此题考查了平行四边形的性质以及相似三角形的判定与性质.注意相似三角形的周长的比等于相似比、高相等的三角形的面积比等于对应底的比.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
13.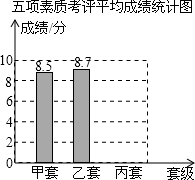 我县某校通过初评决定最后从甲、乙、丙三个班中推荐一个班为校先进班集体,下表是这三个班的五项素质考核表:五项成绩素质考评得分表(单位:分)
我县某校通过初评决定最后从甲、乙、丙三个班中推荐一个班为校先进班集体,下表是这三个班的五项素质考核表:五项成绩素质考评得分表(单位:分)
根据统计表中的信息下列问题:
(1)请你补全五项成绩考评分析表中的数据;
五项成绩考评分析表(单位:分)
(2)参照上表中的数据,你认为应该推荐哪个班为校先进班级?并说明理由;
(3)如果学校把行为规范、学习成绩、校运动会、艺术获奖、劳动卫生五项考评成绩按3:2:1:1:3的权重确定,林老师根据这个总评成绩.绘制了一幅不完整的条形统计图,请将这个统计图补充完整,依照这个成绩,你应推荐哪个班为校先进班集体?
 我县某校通过初评决定最后从甲、乙、丙三个班中推荐一个班为校先进班集体,下表是这三个班的五项素质考核表:五项成绩素质考评得分表(单位:分)
我县某校通过初评决定最后从甲、乙、丙三个班中推荐一个班为校先进班集体,下表是这三个班的五项素质考核表:五项成绩素质考评得分表(单位:分)| 班级 | 行为规范 | 学习成绩 | 校运动会 | 艺术获奖 | 劳动卫生 |
| 甲 | 10 | 10 | 7 | 10 | 6 |
| 乙 | 10 | 8 | 8 | 9 | 8 |
| 丙 | 9 | 10 | 9 | 6 | 9 |
(1)请你补全五项成绩考评分析表中的数据;
五项成绩考评分析表(单位:分)
| 班级 | 平均数 | 众数 | 中位数 |
| 甲 | 8.6 | 10 | 10 |
| 乙 | 8.6 | 8 | 8 |
| 丙 | 8.6 | 9 | 9 |
(3)如果学校把行为规范、学习成绩、校运动会、艺术获奖、劳动卫生五项考评成绩按3:2:1:1:3的权重确定,林老师根据这个总评成绩.绘制了一幅不完整的条形统计图,请将这个统计图补充完整,依照这个成绩,你应推荐哪个班为校先进班集体?
10.关于x的方程mx2-$\sqrt{5-m}$x-1=0有两个实数解,则m的取值范围是( )
| A. | m≥-$\frac{5}{3}$ | B. | 0<m≤5 | C. | -$\frac{5}{3}$≤m≤5且m≠0 | D. | 0<m≤5且m≠0 |
11.下列运算正确的是( )
| A. | (-a2)2=-a4 | B. | $\sqrt{3}$+$\sqrt{4}$=2$\sqrt{3}$ | C. | (π-2)0=0 | D. | ($\frac{1}{3}$)-2=9 |
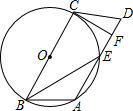 如图,已知在四边形ABCD中,∠ABC=∠D,过A、B、C三点作⊙O交AD于点E,C是$\widehat{AEB}$的中点,CF⊥AD于点F.
如图,已知在四边形ABCD中,∠ABC=∠D,过A、B、C三点作⊙O交AD于点E,C是$\widehat{AEB}$的中点,CF⊥AD于点F.