题目内容
8.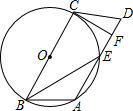 如图,已知在四边形ABCD中,∠ABC=∠D,过A、B、C三点作⊙O交AD于点E,C是$\widehat{AEB}$的中点,CF⊥AD于点F.
如图,已知在四边形ABCD中,∠ABC=∠D,过A、B、C三点作⊙O交AD于点E,C是$\widehat{AEB}$的中点,CF⊥AD于点F.(1)若∠BEA=30°,AB=3,求⊙O的半径;
(2)若BE=5,AE=3,求DF的长.
分析 (1)连接OA、OB,根据同弧所对的圆周角等于圆心角的一半求出∠AOB的度数,然后根据有一个角为60°等腰三角形是等边三角形,判断△AOB为等边三角形,进而可求半径的长;
(2)连接AC、CE,由圆内接四边形的性质可得:∠CED=∠ABC,然后根据等量代换可得:∠D=∠CED,然后根据等角对等边可得CD=CE,然后根据等腰三角形的三线合一,可得DF=$\frac{1}{2}$DE,然后根据AAS判断△CBE≌△CAD可得:BE=AD=5,进而可求DF的长.
解答 (1)解:连接OA、OB,如图1,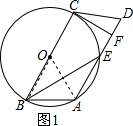
∵∠BEA=30°
∴∠BOA=60°
又∵OB、OA都是半径
∴OA=OB
∴△AOB为等边三角形
∴OB=AB=3
∴半径为3
(2)连接CE,AC,如图2,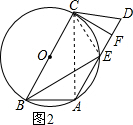
∴∠ABC=∠CED,
∵C是$\widehat{AEB}$的中点,
∴AC=BC,
∴∠ABC=∠BAC=∠BEC,∠D=∠ABC=∠CED,
∴△CED为等腰三角形,
∵CF⊥AD,
∴DF=EF=$\frac{1}{2}$DE,
在△CBE和△CAD中
∵$\left\{\begin{array}{l}{∠D=∠CEB}\\{∠CBE=∠CAD}\\{CB=CA}\end{array}\right.$,
∴△CBE≌△CAD(AAS)
∴BE=AD=5,
∴DF=$\frac{1}{2}$DE=$\frac{1}{2}$(AD-AE)=$\frac{1}{2}$(5-3)=1.
点评 此题考查了圆周角定理,等边三角形的判定,三角形全等的判定,等腰三角形判定与性质,圆内接四边形的性质等知识点,解题的关键是:正确的添加辅助线解决问题.

练习册系列答案
相关题目
3.若实数x满足x-$\frac{1}{x}$=1,则$\frac{{x}^{2}}{{x}^{4}+{x}^{2}+1}$的值是( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{1±\sqrt{5}}{2}$ | D. | $\frac{1+\sqrt{5}}{2}$ |
19.已知△ABC∽△A′B′C′,且相似比为3,则下列结论正确的是( )
| A. | AB是A′B′的3倍 | B. | A′B′是AB的3倍 | C. | ∠A是∠A′的3倍 | D. | ∠A′是∠A的3倍 |
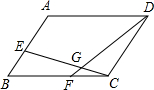 如图,若平行四边形ABCD的面积是1,E在AB上,F在BC上,且AE:EB=5:3,BF:FC=3:2,EC和FD相交于G,则△GFC的面积为$\frac{3}{115}$.
如图,若平行四边形ABCD的面积是1,E在AB上,F在BC上,且AE:EB=5:3,BF:FC=3:2,EC和FD相交于G,则△GFC的面积为$\frac{3}{115}$.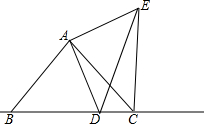 如图,△ABC为等腰直角三角形,AB=AC,∠BAC=90°
如图,△ABC为等腰直角三角形,AB=AC,∠BAC=90°