题目内容
11.以方程组$\left\{\begin{array}{l}{3x-y+a-2=0}\\{2x+y-2a=0}\end{array}\right.$的解为坐标的点在第四象限,求a的取值范围.分析 先把a当作已知数求出方程组的解,再根据第四象限内点的坐标特征已知得出不等式组,求出不等式组的解集即可.
解答 解:$\left\{\begin{array}{l}{3x-y+a-2=0①}\\{2x+y-2a=0②}\end{array}\right.$,
①+②得:5x-a-2=0,
x=$\frac{1}{5}$(a+2),
②×3-①×2得:5y-8a+4=0,
y=$\frac{1}{5}$(8a-4),
∵以方程组$\left\{\begin{array}{l}{3x-y+a-2=0}\\{2x+y-2a=0}\end{array}\right.$的解为坐标的点在第四象限,
∴$\frac{1}{5}$(a+2)>0且$\frac{1}{5}$(8a-4)<0,
解得:-2<a<$\frac{1}{2}$.
点评 本题考查了一次函数与二元一次方程(组),解二元一次方程组,解不等式组的应用,关键是能正确求出方程组的解.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
2.一个直角三角形两条直角边的长分别为4,8,另一个和它相似的直角三角形的一条直角边为12,则另一条直角边的长为( )
| A. | 6 | B. | 24 | C. | 6或24 | D. | 6$\sqrt{5}$或$\sqrt{10}$ |
3.若实数x满足x-$\frac{1}{x}$=1,则$\frac{{x}^{2}}{{x}^{4}+{x}^{2}+1}$的值是( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{1±\sqrt{5}}{2}$ | D. | $\frac{1+\sqrt{5}}{2}$ |
2.实数-27的立方根是( )
| A. | -3 | B. | ±3 | C. | 3 | D. | -$\frac{1}{3}$ |
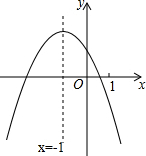 二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:
二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论: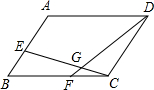 如图,若平行四边形ABCD的面积是1,E在AB上,F在BC上,且AE:EB=5:3,BF:FC=3:2,EC和FD相交于G,则△GFC的面积为$\frac{3}{115}$.
如图,若平行四边形ABCD的面积是1,E在AB上,F在BC上,且AE:EB=5:3,BF:FC=3:2,EC和FD相交于G,则△GFC的面积为$\frac{3}{115}$.