题目内容
10.关于x的方程mx2-$\sqrt{5-m}$x-1=0有两个实数解,则m的取值范围是( )| A. | m≥-$\frac{5}{3}$ | B. | 0<m≤5 | C. | -$\frac{5}{3}$≤m≤5且m≠0 | D. | 0<m≤5且m≠0 |
分析 首先根据方程有两个根可知m≠0,然后根据二次根式的意义以及根的判别式的意义列出关于m的不等式,求出m的取值范围即可.
解答 解:∵关于x的方程mx2-$\sqrt{5-m}$x-1=0有两个实数解,
∴△≥0且m≠0,
∴(-$\sqrt{5-m}$)2-4m(-1)≥0且m≠0,
∴5-m≥0,(5-m)+4m≥0且m≠0,
∴-$\frac{5}{3}$≤m≤5且m≠0,
故选:C.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根,解答此题要注意一元二次方程的二次项系数不能为0以及二次根式有意义的条件,此题难度不大.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
2.实数-27的立方根是( )
| A. | -3 | B. | ±3 | C. | 3 | D. | -$\frac{1}{3}$ |
19.已知△ABC∽△A′B′C′,且相似比为3,则下列结论正确的是( )
| A. | AB是A′B′的3倍 | B. | A′B′是AB的3倍 | C. | ∠A是∠A′的3倍 | D. | ∠A′是∠A的3倍 |
20.若a=-2,则a的绝对值是( )
| A. | 2 | B. | -2 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
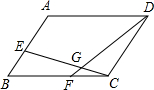 如图,若平行四边形ABCD的面积是1,E在AB上,F在BC上,且AE:EB=5:3,BF:FC=3:2,EC和FD相交于G,则△GFC的面积为$\frac{3}{115}$.
如图,若平行四边形ABCD的面积是1,E在AB上,F在BC上,且AE:EB=5:3,BF:FC=3:2,EC和FD相交于G,则△GFC的面积为$\frac{3}{115}$.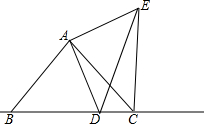 如图,△ABC为等腰直角三角形,AB=AC,∠BAC=90°
如图,△ABC为等腰直角三角形,AB=AC,∠BAC=90°
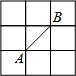 如图所示的正方形网格中,网格线的交点称为格点,已知A、B 两点为格点,如果C也是图中的格点,则满足△ABC为等腰三角形的点C的个数为( )
如图所示的正方形网格中,网格线的交点称为格点,已知A、B 两点为格点,如果C也是图中的格点,则满足△ABC为等腰三角形的点C的个数为( )