题目内容
5．已知k是整数，x2+kxy-6y2能因式分解，那么所有满足条件的k有4个，它们的和是0．分析 根据十字相乘法分解，可得k的值，根据有理数的加法，可得和．
解答 解：x2+kxy-6y2=（x+y）（x-6y），k=1+（-6）=-5，
x2+kxy-6y2=（x-y）（x+6y），k=-1+6=5，
x2+kxy-6y2=（x-2y）（x+3y），k=-2+3=1，
x2+kxy-6y2=（x-3y）（x+2y），k=-3+2=-1，
k有4个，
它们的和是-5+5+（-1）+1=0，
故答案为：4，0．
点评 本题考查了因式分解，利用十字相乘法分解是解题关键．
练习册系列答案
能力评价系列答案
唐印文化课时测评系列答案
导学与测试系列答案
相关题目
16．下列各图中，正确画出AC边上的高的是（ ）
| A． |  | B． |  | ||
| C． |  | D． |  |
20．一小球以15m/s的初始速度竖直向上弹出，它在空中的高度h（m）与时间t（s）满足关系式：h=15t-5t2．
（1）填写下表：
（2）你能根据表格中的数据猜测何时小球达到最高处吗？
（1）填写下表：
| t/s | 0.25 | 0.5 | 1 | 1.25 | 1.5 | 1.75 | 2 | 2.25 |
| h/m | 3.4375 | 6.25 | 10 | 10.9375 | 11.25 | 10.9375 | 10 | 8.4375 |
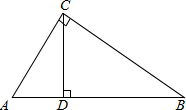已知：如图，在Rt△ABC中，CD是斜边AB上高，找出图中的相似三角形．并说明理由．
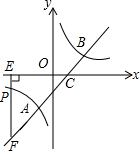如图，直线y=x-1与反比例函数y=$\frac{k}{x}$的图象交于A，B两点，与x轴交于点C，已知点A的横坐标为-1．