题目内容
15.已知$\frac{2a-b}{a+b}$=5,求$\frac{2(2a-b)}{a+b}$+$\frac{3(a+b)}{2a-b}$的值.分析 由$\frac{2a-b}{a+b}$=5,可得$\frac{2(2a-b)}{a+b}$+$\frac{3(a+b)}{2a-b}$=2×5+3×$\frac{1}{5}$求解即可.
解答 解:∵$\frac{2a-b}{a+b}$=5,
∴$\frac{2(2a-b)}{a+b}$+$\frac{3(a+b)}{2a-b}$=2×5+3×$\frac{1}{5}$=10+$\frac{3}{5}$=10$\frac{3}{5}$.
点评 本题主要考查了分式的化简求值,解题的关键是求出$\frac{2a-b}{a+b}$的式子

练习册系列答案
相关题目
3.化简$\frac{{a}^{2}+2ab+{b}^{2}}{{a}^{2}-{b}^{2}}$的结果是( )
| A. | $\frac{a+b}{a-b}$ | B. | $\frac{b}{a-b}$ | C. | $\frac{a}{a+b}$ | D. | $\frac{b}{a+b}$ |
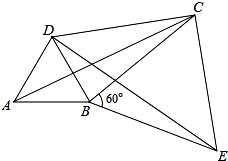 给出定义,若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称该四边形为勾股四边形.
给出定义,若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称该四边形为勾股四边形.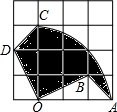 如图,在4×4的正方形网格中,每个小正方形的边长均为1,将△AOB绕点O逆时针旋转90°得到△COD,则旋转过程中形成的阴影部分的面积为$\frac{9}{4}π$.
如图,在4×4的正方形网格中,每个小正方形的边长均为1,将△AOB绕点O逆时针旋转90°得到△COD,则旋转过程中形成的阴影部分的面积为$\frac{9}{4}π$. 一个圆柱被裁成几部分,如图是其中一个部分,求它的侧面积(可以试着剪一剪,看看它的侧面展开图)
一个圆柱被裁成几部分,如图是其中一个部分,求它的侧面积(可以试着剪一剪,看看它的侧面展开图)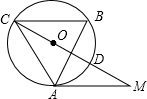 如图,在△ABC中,∠B=60°,⊙O是△ABC的外接圆,过点A作⊙O的切线,交CO的延长线于点M,CM交⊙O于点D.
如图,在△ABC中,∠B=60°,⊙O是△ABC的外接圆,过点A作⊙O的切线,交CO的延长线于点M,CM交⊙O于点D.