题目内容
4.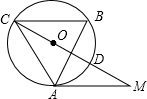 如图,在△ABC中,∠B=60°,⊙O是△ABC的外接圆,过点A作⊙O的切线,交CO的延长线于点M,CM交⊙O于点D.
如图,在△ABC中,∠B=60°,⊙O是△ABC的外接圆,过点A作⊙O的切线,交CO的延长线于点M,CM交⊙O于点D.(1)求证:AM=AC;
(2)若AC=3,求MC的长.
分析 (1)连接OA,根据圆周角定理求出∠AOC=120°,得到∠OCA的度数,根据切线的性质求出∠M的度数,根据等腰三角形的性质得到答案;
(2)作AG⊥CM于G,根据直角三角形的性质求出AG的长,根据勾股定理求出CG,得到答案.
解答 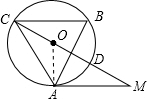 (1)证明:连接OA,
(1)证明:连接OA,
∵AM是⊙O的切线,∴∠OAM=90°,
∵∠B=60°,∴∠AOC=120°,
∵OA=OC,∴∠OCA=∠OAC=30°,
∴∠AOM=60°,∴∠M=30°,
∴∠OCA=∠M,
∴AM=AC;
(2)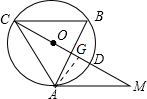 作AG⊥CM于G,
作AG⊥CM于G,
∵∠OCA=30°,AC=3,∴AG=$\frac{3}{2}$,
由勾股定理的,CG=$\frac{3\sqrt{3}}{2}$,
则MC=2CG=3$\sqrt{3}$.
点评 本题考查的是切线的性质、等腰三角形的性质和勾股定理的应用,掌握圆的切线垂直于过切点的半径是解题的关键.

练习册系列答案
相关题目
14.计算:1252-50×125+252=( )
| A. | 100 | B. | 150 | C. | 10000 | D. | 22500 |
9.若(ax2-2xy+y2)-(-ax2+bxy+2y2)=6x2-9xy+cy2成立,则a,b,c的值分别为( )
| A. | 3,-7,-1 | B. | -3,7,-1 | C. | 3,7,-1 | D. | -3,-7,1 |
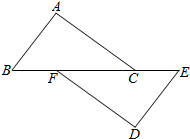 如图,点B,F,C,E在同一直线上,BF=CE,AB∥DE,请添加一个条件,使△ABC≌△DEF,这个添加的条件可以是AB=DE(只需写一个,不添加辅助线).
如图,点B,F,C,E在同一直线上,BF=CE,AB∥DE,请添加一个条件,使△ABC≌△DEF,这个添加的条件可以是AB=DE(只需写一个,不添加辅助线).