题目内容
18.已知正三角形的内切圆半径为$\frac{\sqrt{3}}{3}$cm,则它的边长是( )| A. | 2cm | B. | $\frac{4}{3}$cm | C. | 2$\sqrt{3}$cm | D. | $\sqrt{3}$cm |
分析 首先根据题意画出图形,由O是△ABC的内心,可求得∠OAD=30°,又由正三角形的性质,即可求得正三角形的边长.
解答 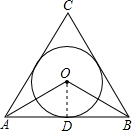 解:过O点作OD⊥AB,则OD=$\frac{\sqrt{3}}{3}$;
解:过O点作OD⊥AB,则OD=$\frac{\sqrt{3}}{3}$;
∵O是△ABC的内心,
∴∠OAD=30°;
Rt△OAD中,∠OAD=30°,OD=$\frac{\sqrt{3}}{3}$,
∴AD=$\frac{OD}{tan30°}$=$\frac{\frac{\sqrt{3}}{3}}{\frac{\sqrt{3}}{3}}$=1,
∴AB=2AD=2.
故选A.
点评 此题考查了三角形内切圆的性质.此题难度不大,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
3. 如图是赛车跑道的一部分路段,已知AB∥CD,则∠A=110°,∠E=80°,则∠D的度数为( )
如图是赛车跑道的一部分路段,已知AB∥CD,则∠A=110°,∠E=80°,则∠D的度数为( )
 如图是赛车跑道的一部分路段,已知AB∥CD,则∠A=110°,∠E=80°,则∠D的度数为( )
如图是赛车跑道的一部分路段,已知AB∥CD,则∠A=110°,∠E=80°,则∠D的度数为( )| A. | 40° | B. | 30° | C. | 20° | D. | 10° |
7.已知-2<m<3,化简$\sqrt{(m-3)^{2}}$+|m+2|的结果是( )
| A. | 5 | B. | 1 | C. | 2m-1 | D. | 2m-5 |
8.下列各组数中不能作为直角三角形的三边长的是( )
| A. | 5,12,14 | B. | 6,8,10 | C. | 7,24,25 | D. | 8,15,17 |
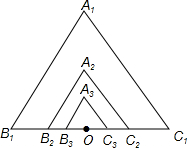 如图所示,由位似的正△A1B1C1,正△A2B2C2,正△A3B3C3,…正△AnBnCn组成的相似图形,其中第一个△A1B1C1的边长为1,点O是B1C1中点,A2是OA1的中点,A3是OA2的中点…An是OAn-1的中点,顶点B2,B3,…,Bn.C2,C3,…,Cn都在B1C1边上.
如图所示,由位似的正△A1B1C1,正△A2B2C2,正△A3B3C3,…正△AnBnCn组成的相似图形,其中第一个△A1B1C1的边长为1,点O是B1C1中点,A2是OA1的中点,A3是OA2的中点…An是OAn-1的中点,顶点B2,B3,…,Bn.C2,C3,…,Cn都在B1C1边上.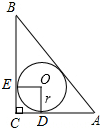 如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,则△ABC的内切圆半径r=1.
如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,则△ABC的内切圆半径r=1.
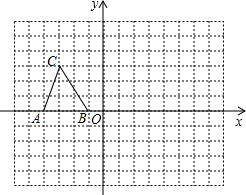 如图,在平面直角坐标系中(网格正方形的边长为1个单位),已知△ABC三个顶点的坐标分别为A(-4,0),B(-1,0),C(-3,3).
如图,在平面直角坐标系中(网格正方形的边长为1个单位),已知△ABC三个顶点的坐标分别为A(-4,0),B(-1,0),C(-3,3).