题目内容
13.如图1,D、E、F分别是△ABC三边AB、BC和AC上的点,若∠1=∠2,∠3=∠4,∠5=∠6,我们称△DEF为△ABC的反射三角形.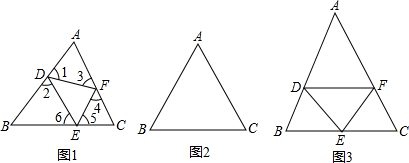
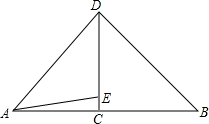
(1)若△ABC是正三角形(如图2),猜想其反射三角形的形状,并画出图形加以说明;
(2)如图3,△DEF是△ABC的反射三角形,AB=AC,∠A=50°,求△DEF各个角的度数;
(3)利用图1探究:
①△ABC的三个内角与其反射三角形DEF的对应角(如∠DEF与∠A)之间的数量关系;
②在直角三角形和钝角三角形中,是否存在反射三角形?如果存在,说出其反射三角形的形状;如果不存在,说明理由.
分析 (1)根据正三角形的反射三角形的关系,可得反射三角形的内角的度数,可得答案;
(2)根据三角形内角和定理,可得∠B=∠C,根据三角形内角和定理,可得关于x的方程,根据平角的定义,可得答案;
(3)①根据三角形内角和定理,可得∠3、∠5的表示,根据三角形内角和定理,可得∠1与∠C的关系,根据根据平角的定义,可得答案;
②根据反射三角形对角的关系,可得答案.
解答 解:(1)如图2,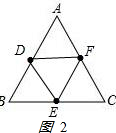
△ABC是正三角形,其反射△DEF是正三角形,理由如下:
∠A=∠BED=∠FED=60°,
同理∠B=∠EFC=∠AFD=∠DFE=60°,
∠C=∠BDE=∠ADF=∠EDF=60°,
∠FED=DFE=∠EDF=60°,
∴△DEF是正三角形
(2)如图3: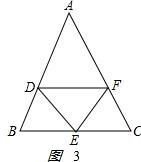
在△ABC中,由三角形内角和定理,得
∠B=∠C=(180°-∠A)÷2=65°,
设∠ADF=∠BDE=x°,
在△ADF和△BDE中,由三角形的内角和定理,得
∠CFE=∠AFD=180°-∠A-x°,
∠FEC=∠BED=180°-∠B-x°,
在△CEF中,由三角形的内角和定理,得∠CFE+∠FEC+∠C=180°,
即180°-∠A-x°+180°-∠B-x°+∠C=180°,
解得x=65,∠CFE=∠AFD=180°-50°-65°=65°,∠FEC=∠BED=180°-65°-65°=50°.
由平角的定义,得
∠EDF=180°-∠ADF-∠BDE=180°-65°-65°=50°,
∠DEF=180°-∠BED-∠CEF=180°-50°-50°=80°,
∠DFE=180°-∠AFD-∠CFE=180°-65°-65°=50°;
(3)如图1,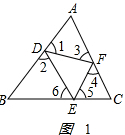 ,
,
①∠1=∠2=x°,
在△ADF和△BDE中,由三角形的内角和定理,得
∠3=∠4=180°-∠A-x°,
∠5=∠6=180°-∠B-x°,
由三角形的内角和定理,得∠4+∠5+∠C=180°,
即180°-∠A-x°+180°-∠B-x°+∠C=180°,
解得x=∠C,
∠EDF+2∠C=180°,∠DEF+2∠A=180°,∠DFE+2∠C=180°;
②在直角三角形中,不存在反射三角形,理由如下:
当∠C=90°时,∠EDF+2∠C=180°,得∠EDF=0°,
∴直角三角形中,不存在反射三角形;
在钝角三角形中,不存在反射三角形,理由如下:
当∠C>90°时,∠EDF+2∠C=180°,得∠EDF<0°,
∴在钝角三角形中,不存在反射三角形.
点评 本题考查了三角形边角关系,利用了三角形内角和定理,平角的定义,利用三角形内角和得出∠4、∠6、∠1的关系是解题关键.

| A. | 2cm | B. | $\frac{4}{3}$cm | C. | 2$\sqrt{3}$cm | D. | $\sqrt{3}$cm |
 重庆市是著名的山城,许多美丽的建筑建在山上,如图,刘老师为了测量小山项一建筑物DE的高度,和潘老师一起携带测量装备前往测量.刘老师在山脚下的A处测得建筑物顶端D的仰角为53°,山坡AE的坡度i=1:5,潘老师在B处测得建筑物顶端D的仰角为45°.若此时刘老师与潘老师的距离AB=200m,求建筑物DE的高度.(sin53°≈$\frac{4}{5}$,cos53°≈$\frac{3}{5}$,tan53°≈$\frac{4}{3}$,结果精确到0.1m)
重庆市是著名的山城,许多美丽的建筑建在山上,如图,刘老师为了测量小山项一建筑物DE的高度,和潘老师一起携带测量装备前往测量.刘老师在山脚下的A处测得建筑物顶端D的仰角为53°,山坡AE的坡度i=1:5,潘老师在B处测得建筑物顶端D的仰角为45°.若此时刘老师与潘老师的距离AB=200m,求建筑物DE的高度.(sin53°≈$\frac{4}{5}$,cos53°≈$\frac{3}{5}$,tan53°≈$\frac{4}{3}$,结果精确到0.1m)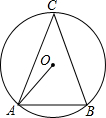 如图,⊙O是△ABC的外接圆,C是优弧AB上一点,设∠OAB=α,∠C=β.
如图,⊙O是△ABC的外接圆,C是优弧AB上一点,设∠OAB=α,∠C=β.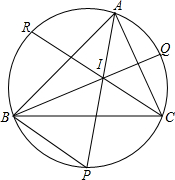 如图5,I是△ABC的内心,且∠A、∠B、∠C的平分线延长线分别交外接圆于P,Q,R点.
如图5,I是△ABC的内心,且∠A、∠B、∠C的平分线延长线分别交外接圆于P,Q,R点.