题目内容
3. 如图是赛车跑道的一部分路段,已知AB∥CD,则∠A=110°,∠E=80°,则∠D的度数为( )
如图是赛车跑道的一部分路段,已知AB∥CD,则∠A=110°,∠E=80°,则∠D的度数为( )| A. | 40° | B. | 30° | C. | 20° | D. | 10° |
分析 过E点作EF∥AB,如图,由于AB∥CD,则EF∥CD,根据平行线的性质得到∠1+∠A=180°,∠2=∠D,则可先计算出∠1=180°-∠A=70°,再利用∠1+∠2=80°可计算出∠2=10°,于是可得到∠D=10°.
解答 解:过E点作EF∥AB,如图,
∵AB∥CD,
∴EF∥CD,
∴∠1+∠A=180°,∠2=∠D,
∴∠1=180°-110°=70°,
而∠1+∠2=80°,
∴∠2=10°,
∴∠D=10°.
故选D.
点评 本题考查了平行线性质:两直线平行,同位角相等;两直线平行,同旁内角互补;两直线平行,内错角相等.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
18.已知正三角形的内切圆半径为$\frac{\sqrt{3}}{3}$cm,则它的边长是( )
| A. | 2cm | B. | $\frac{4}{3}$cm | C. | 2$\sqrt{3}$cm | D. | $\sqrt{3}$cm |
8.在平面直角坐标系中,将点A(-3,4)向右平移5个单位长度后,那么平移后对应的点A′的坐标是( )
| A. | (-3,-4) | B. | (2,4) | C. | (-3,9) | D. | (2,-1) |
15.(-2)2014+3×(-2)2013的值为( )
| A. | -22013 | B. | 22013 | C. | 22014 | D. | 22014 |
13.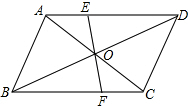 如图.点O是?ABCD两条对角线的交点,过O点的直线分别交AD、BC于E、F,则图中全等的三角形共有( )
如图.点O是?ABCD两条对角线的交点,过O点的直线分别交AD、BC于E、F,则图中全等的三角形共有( )
 如图.点O是?ABCD两条对角线的交点,过O点的直线分别交AD、BC于E、F,则图中全等的三角形共有( )
如图.点O是?ABCD两条对角线的交点,过O点的直线分别交AD、BC于E、F,则图中全等的三角形共有( )| A. | 3对 | B. | 4对 | C. | 6对 | D. | 8对 |
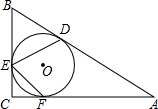 如图,在Rt△ABC中,∠C=90°,∠B=70°,△ABC的内切圆⊙O与边AB、BC、CA分别相切于点D、E、F,则∠DEF的度数为80°.
如图,在Rt△ABC中,∠C=90°,∠B=70°,△ABC的内切圆⊙O与边AB、BC、CA分别相切于点D、E、F,则∠DEF的度数为80°.