题目内容
19.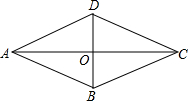 已知:如图,在四边形ABCD中,对角线AC、BD交于点O,线段BD垂直平分AC,DC∥AB.
已知:如图,在四边形ABCD中,对角线AC、BD交于点O,线段BD垂直平分AC,DC∥AB.求证:四边形ABCD是菱形.
分析 根据ASA可证△AOB≌△COD,根据全等三角形的性质可得AB=CD,可得四边形ABCD是平行四边形,再根据线段垂直平分线的性质可得AD=CD,再根据菱形的判定即可求解.
解答 证明:∵DC∥AB,
∴∠OAB=∠OCD,∠OBA=∠ODC,
∵线段BD垂直平分AC,
∴OA=OC,AD=CD,
在△AOB与△COD中,
$\left\{\begin{array}{l}{∠OBA=∠ODC}\\{∠OAB=∠OCD}\\{OA=OC}\end{array}\right.$,
∴△AOB≌△COD,
∴AB=CD,
∴四边形ABCD是平行四边形,
∵AD=CD,
∴四边形ABCD是菱形.
点评 此题考查了菱形的判定、平行四边形的判定与性质以及线段垂直平分线的性质.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
7.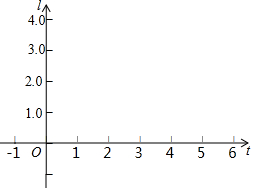 某学生发现学校的电动伸缩门从宪全收拢到完全打开的过程中,电动伸缩门伸缩后的总长度1(米)与按电钮开关的时间t(秒)之间存在某种函数关系(电动伸缩门初始状态是完全收拢的).经几次试验后,得到一组对应数据如下:
某学生发现学校的电动伸缩门从宪全收拢到完全打开的过程中,电动伸缩门伸缩后的总长度1(米)与按电钮开关的时间t(秒)之间存在某种函数关系(电动伸缩门初始状态是完全收拢的).经几次试验后,得到一组对应数据如下:
(1)请你在已建立的平面直角坐标系中,通过①描点、连线,②猜测l与t之间的函数关系,③求出函数的解析式,④验证,这四个步骤确定l与t之间的函数关系;
(2)已知学校的大门宽为5米,问将校门完全关闭再完全打开共用多少秒?
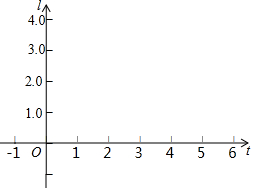 某学生发现学校的电动伸缩门从宪全收拢到完全打开的过程中,电动伸缩门伸缩后的总长度1(米)与按电钮开关的时间t(秒)之间存在某种函数关系(电动伸缩门初始状态是完全收拢的).经几次试验后,得到一组对应数据如下:
某学生发现学校的电动伸缩门从宪全收拢到完全打开的过程中,电动伸缩门伸缩后的总长度1(米)与按电钮开关的时间t(秒)之间存在某种函数关系(电动伸缩门初始状态是完全收拢的).经几次试验后,得到一组对应数据如下:| t(秒) | 0 | 1 | 2 | 3 | 4 | 5 | … |
| l(米) | 1 | 1.4 | 1.8 | 2.2 | 2.6 | 3.0 | … |
(2)已知学校的大门宽为5米,问将校门完全关闭再完全打开共用多少秒?
9.从一副洗匀的普通扑克牌中随机抽取一张,则抽出红桃的概率是( )
| A. | $\frac{1}{54}$ | B. | $\frac{13}{54}$ | C. | $\frac{1}{13}$ | D. | $\frac{1}{4}$ |
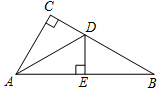 如图,在Rt△ABC中,∠C=90°,AD平分∠CAB,交CB于点D,DE⊥AB于点E.
如图,在Rt△ABC中,∠C=90°,AD平分∠CAB,交CB于点D,DE⊥AB于点E.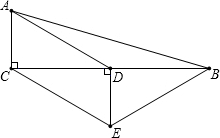 如图,在△ABC中,∠ACB=90°,D是BC的中点,DE⊥BC,垂足为点D,CE∥AD,若AC=2,CE=4.
如图,在△ABC中,∠ACB=90°,D是BC的中点,DE⊥BC,垂足为点D,CE∥AD,若AC=2,CE=4.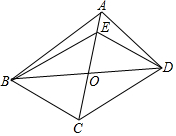 如图,在四边形ABCD中,对角线AC、BD相交于点O,且OB=OD,点E在线段OA上,连接BE,DE.给出下列条件:①OC=OE;②AB=AD;③BC⊥CD;④∠CBD=∠EBD.请你从中选择两个条件,使四边形BCDE是菱形,并给予证明.你选择的条件是①②(只填写序号).
如图,在四边形ABCD中,对角线AC、BD相交于点O,且OB=OD,点E在线段OA上,连接BE,DE.给出下列条件:①OC=OE;②AB=AD;③BC⊥CD;④∠CBD=∠EBD.请你从中选择两个条件,使四边形BCDE是菱形,并给予证明.你选择的条件是①②(只填写序号).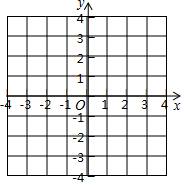 在平面直角坐标系xOy中,抛物线y=-x2+2mx-3+4m-m2的对称轴是直线x=1
在平面直角坐标系xOy中,抛物线y=-x2+2mx-3+4m-m2的对称轴是直线x=1 在Rt△ABC中,∠C=90°,∠A=30°,AB=6,点D,E分别是BC,AB上的动点,将△BDE沿直线DE翻折,点B的对应点B′恰好落在AC上,若△AEB′是等腰三角形,那么CB′的值是3,3$\sqrt{2}$-3,0.
在Rt△ABC中,∠C=90°,∠A=30°,AB=6,点D,E分别是BC,AB上的动点,将△BDE沿直线DE翻折,点B的对应点B′恰好落在AC上,若△AEB′是等腰三角形,那么CB′的值是3,3$\sqrt{2}$-3,0.