题目内容
13.设a,b是任意两个不等实数,我们规定:满足不等式a≤x≤b的实数x的所有取值的全体叫做闭区间,表示为[a,b].对于一个函数,如果它的自变量x与函数值y满足:当m≤x≤n时,有m≤y≤n,我们就称此函数是闭区间[m.n]上的“闭函数”.如函数y=-x+4,当x=1时,y=3;当x=3时,y=1,即当1≤x≤3时,有1≤y≤3,所以说函数y=-x+4是闭区间[1,3]上的“闭函数”.(1)反比例函数y=$\frac{2015}{x}$是闭区间[1,2015]上的“闭函数”吗?请判断并说明理由;
(2)若二次函数y=x2-2x-k是闭区间[1,2]上的“闭函数”,求k的值;
(3)若一次函数y=kx+b(k≠0)是闭区间[m,n]上的“闭函数”,求此函数的解析式(用含m,n的代数式表示).
分析 (1)根据反比例函数y=$\frac{2015}{x}$的单调区间进行判断;
(2)由于二次函数y=x2-2x-k的图象开口向上,对称轴为x=1,所以二次函数y=x2-2x-k在闭区间[1,2]内,y随x的增大而增大.当x=1时,y=1,所以k=-2.当x=2时,y=2,所以k=-2.即图象过点(1,1)和(2,2),所以当1≤x≤2时,有1≤y≤2,符合闭函数的定义,所以k=-2.
(3)根据新定义运算法则,分两种情况:k>0,k<0,列出关于系数k、b的方程组,通过解该方程组即可求得系数k、b的值,即可解答.
解答 解:(1)反比例函数y=$\frac{2015}{x}$是闭区间[1,2015]上的“闭函数”.理由如下:
反比例函数y=$\frac{2015}{x}$在第一象限,y随x的增大而减小,
当x=1时,y=2015;
当x=2015时,y=1,
即图象过点(1,2015)和(2015,1)
∴当1≤x≤2015时,有1≤y≤2015,符合闭函数的定义,
∴反比例函数y=$\frac{2015}{x}$是闭区间[1,2015]上的“闭函数”;
(2)由于二次函数y=x2-2x-k的图象开口向上,
对称轴为x=1,
∴二次函数y=x2-2x-k在闭区间[1,2]内,y随x的增大而增大.
当x=1时,y=1,
∴k=-2;
当x=2时,y=2,
∴k=-2;
即图象过点(1,1)和(2,2),
∴当1≤x≤2时,有1≤y≤2,符合闭函数的定义,
∴k=-2.
(3)因为一次函数y=kx+b(k≠0)是闭区间[m,n]上的“闭函数”,
根据一次函数的图象与性质,有:
(Ⅰ)当k>0时,即图象过点(m,m)和(n,n),
$\left\{\begin{array}{l}{mk+b=m}\\{nk+b=n}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=1}\\{b=0}\end{array}\right.$,
∴y=x;
(Ⅱ)当k<0时,即图象过点(m,n)和(n,m),
可得:$\left\{\begin{array}{l}{mk+b=n}\\{nk+b=m}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-1}\\{b=m+n}\end{array}\right.$,
∴y=-x+m+n,
∴一次函数的解析式为y=x或y=-x+m+n.
点评 本题考查的是反比例函数的性质,解题的关键是弄清楚“闭函数”的定义.解题时,也要注意“分类讨论”数学思想的应用.

 名校课堂系列答案
名校课堂系列答案 如图所示,∠1=∠2,∠2+∠3=180°,试说明:a∥b,c∥d.
如图所示,∠1=∠2,∠2+∠3=180°,试说明:a∥b,c∥d.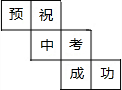 一个正方体的表面展开如图所示,六个面上各有一字,连起来的意思是“预祝中考成功”,把它折成正方体后,与“考”相对的字是( )
一个正方体的表面展开如图所示,六个面上各有一字,连起来的意思是“预祝中考成功”,把它折成正方体后,与“考”相对的字是( )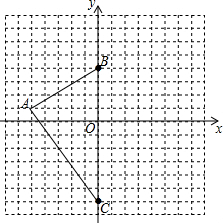 已知△ABC的顶点在坐标系中的坐标分别为:A(-5,1)、B(0,4)、C(0,-6).
已知△ABC的顶点在坐标系中的坐标分别为:A(-5,1)、B(0,4)、C(0,-6).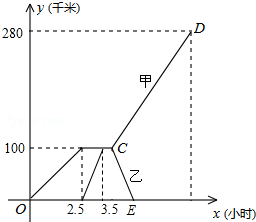 已知,A、B两市相距280千米,甲车从A市前往B市运送物资,行驶2.5小时在M地汽车M地汽车出现故障,立即通知技术人员乘乙车从A市赶来维修(通知时间忽略不计).乙车到达M地后又经过30分钟修好甲车后原路返回,同时甲车以原速1.5倍的速度前往B市.如图是甲、乙两车距A市的路程y(千米)与甲车行驶时间x(小时)之间的函数图象,结合图象回答下列问题:
已知,A、B两市相距280千米,甲车从A市前往B市运送物资,行驶2.5小时在M地汽车M地汽车出现故障,立即通知技术人员乘乙车从A市赶来维修(通知时间忽略不计).乙车到达M地后又经过30分钟修好甲车后原路返回,同时甲车以原速1.5倍的速度前往B市.如图是甲、乙两车距A市的路程y(千米)与甲车行驶时间x(小时)之间的函数图象,结合图象回答下列问题: 如图,在△ABC中,AB=5厘米,BC=3厘米,BM为中线,则△ABM与△BCM的周长之差是2厘米.
如图,在△ABC中,AB=5厘米,BC=3厘米,BM为中线,则△ABM与△BCM的周长之差是2厘米.