题目内容
20.如果3x+1=|2x-3|成立,则x的正数解为x=$\frac{2}{5}$.分析 分类讨论:-$\frac{1}{3}$≤x$≤\frac{3}{2}$,x>$\frac{3}{2}$,根据差的绝对值是大数减小数,可化简绝对值,根据解方程,可得答案.
解答 解:当-$\frac{1}{3}$≤x$≤\frac{3}{2}$时,3x+1=-2x+3,解得x=$\frac{2}{5}$
当x>$\frac{3}{2}$时,3x+1=2x-3,解得x=-4(不符合题意的解要舍去),
综上所述:x=$\frac{2}{5}$,
故答案为:x=$\frac{2}{5}$.
点评 本题考查了含绝对值符号的一元一次方程,分类讨论是解题关键,以防遗漏.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8. 将一个多边形按图所示减掉一个角,所得多边形的内角和为1800°,那么原多边形的边数是( )
将一个多边形按图所示减掉一个角,所得多边形的内角和为1800°,那么原多边形的边数是( )
 将一个多边形按图所示减掉一个角,所得多边形的内角和为1800°,那么原多边形的边数是( )
将一个多边形按图所示减掉一个角,所得多边形的内角和为1800°,那么原多边形的边数是( )| A. | 10 | B. | 11 | C. | 12 | D. | 13 |
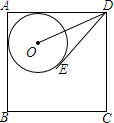 如图,⊙O与正方形ABCD的两边AB、AD相切,且DE与⊙O相切于E点.若正方形ABCD的周长为28,且DE=4,则sin∠ODE=$\frac{3}{5}$.
如图,⊙O与正方形ABCD的两边AB、AD相切,且DE与⊙O相切于E点.若正方形ABCD的周长为28,且DE=4,则sin∠ODE=$\frac{3}{5}$.
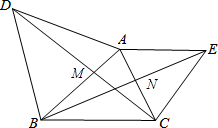 如图,△ABD、△AEC都是等边三角形.AB、CD相交于M,AC、BE相交于N,∠MAN=60°.求证:
如图,△ABD、△AEC都是等边三角形.AB、CD相交于M,AC、BE相交于N,∠MAN=60°.求证: